Árboles y grafos

Vladimir Támara Patiño.

2004. Dominio público. Sin garantías.
Agradecemos que como fuente se cite: http://structio.sourceforge.net/guias/arbgraf/

Este escrito se dedican a nuestro Padre Creador, a su santo Espíritu y a Jesús su Hijo y maestro nuestro.

Capítulo 1   Introducción y definiciones

1.1   Definiciones

Indicadores de logro: En este contexto árboles y grafos se refiere a estructuras de datos que permiten organizar y mantener información en un computador. Esta forma se inspira una forma de organizar información con lápiz y papel usando nodos y flechas entre los nodos (a esas flechas también se les llama arcos, a los nodos también se les llama vértices). Los grafos y árboles en papel son apropiados por ejemplo para capturar sólo una parte de la información de objetos, situaciones y otros tipos de información (i.e son apropiados para abstraer).

En un computador además de permitir organizar información, resultan estructuras útiles para resolver ciertos tipos de problema (por ejemplo pueden emplearse árboles AVL para mantener información ordenada de forma eficiente).

Para jugar, entender y emplear mejor grafos (y árboles) varias personas (e.g Euler) han propuesto definiciones; a partir de estas definiciones y con ayuda de razonamientos lógicos han demostrado propiedades. Un mínimo de definiciones y de propiedades de grafos y árboles (con estilo inspirado en [6]) se presenta a continuación.

Note que para ver mejor esta página puede requerir configurar su navegador para que presente símbolos especiales, que se esperan con el tipo de letra de symbol. En el caso del navegador Mozilla, y suponiendo que en su sistema ya está instalado y configurado para Mozilla el tipo de letra para símbolos marque el botón de chequeo que permite que el documento use otras fuentes, en el menú apariencia del diálogo de preferencias (elemento del menú editar).

1.1.1   Teoría

Grafos

Un grafo G es una pareja G=(V,A), donde V es un conjunto finito (i.e vértices) y A es un subconjunto del conjunto de parejas no ordenadas de V (i.e arcos). Por ejemplo G=({a,b,c},{{a,c},{c,b}}), que se representa gráficamente en la figura 1.1.



Figure 1.1: Ejemplo de grafo


Dado un grafo G con V(G) denotamos el conjunto de vértices y con A(G) denotamos el conjunto de arcos. Decimos que un arco {x,y}Î A(G) une los vértices x e y; así que x,y denota el mismo arco que {y,x}. Si {x,y} es un arco, decimos que x e y son extremos del arco, también decimos que x es adyacente o vecino de y.

Un grafo G'=(V',A') es subgrafo de G=(V,A) si V'Ì V y AÌ A'. En tal caso escribimos G'Ì G.

Si G' contiene todos los arcos de G que unen dos vértices de V' decimos que G' es un subgrafo inducido por V' y se denota por G[V'].

El orden de un grafo G es el número de vértices, también se denota por G 1. El tamaño de G es el número de arcos, y se denota por a(G).

Decimos que dos grafos son isomorfos si hay una correspondencia entre sus conjuntos de vértices que preserva la adyacencia. Así que G=(V,E) es isomorfo a G'=(V',E') si hay una biyección j: V V' tal que x,yÎ E si y solo si j(x)j(y)Î E'. Entonces dos grafos isomorfos tienen el mismo orden y el mismo tamaño.

El tamaño de un grafo de orden n es al menos 0 y a lo sumo ( 2n). Un grafo de orden n y tamaño (2n) se llama un n-grafo completo2 y se denota por Kn; un n-grafo vació En tiene orden n y ningún vértice. En todo Kn todo par de vértices son adyacentes, mientras que en En ningún par de vértices son adyacentes.

El conjunto de vértices adyacentes a un vértice xÎ G, se denota por G(x). El grado de x es g(x)= G(x). El grado mínimo de los vértices de un grafo se denota por d(G), mientras que el grado máximo se denota por D(G). Un vértice de grado 0 se dice que es un vértice aislado. Si d(G)=D(G)=k, es decir todo vértice es de grado k entonces se dice que G es k-regular o regular de grado k. Un grafo es regular si es k-regular para algún k.

Dado que V(G)={x1,x2··· xn}, como todo arco tiene dos vértices extremos, la suma de los grados es exactamente dos veces el número de vértices:
n
å
i=1
g(xi)=2e(G)

Esta observación se llama también el lema de los apretones de manos, pues expresa que en una fiesta el número total de manos apretadas es par. Esto también establece que el número de vértices de grado impar es par.

Un camino W en un grafo G es una secuencia de los vértices de G, (x0,x1,···,xl) tal que {xi,xi+1}Î A(G) para 0£ i<l. A x0 y a xl los llamamos vértices extremos del camino. Un camino en el que todos los vértices son diferentes se denomina sendero. Un sendero en el que los vértices extremos son iguales se denomina un circuito o si l>2 también se denomina un ciclo, y puede denotarse por x1x2··· xl.

Con Cl denotamos un ciclo de longitud l. Llamamos a C3 un triángulo, a C4 un cuadrilátero, a C5 un pentágono, etc.

Dados vértices x, y su distancia d(x,y) es la longitud mínima de un camino de x a y.

Un grafo es conexo si para todo par x, y de vértices diferentes hay un camino de x a y. Note que un grafo conexo de orden al menos 2 no puede tener vértices aislados.

Con la definición que empleamos un grafo no contiene lazos, es decir un arco que una vértice consigo mismo; ni contiene arcos múltiples es decir que varios arcos unan los mismos dos vértices. En un multigrafo se permiten lazos, arcos múltiples y lazos múltiples.

Si los arcos son parejas ordenadas de vértices entonces tenemos la noción de grafo dirigido o multigrafo dirigido. Un pareja ordenada (a,b) se llama un arco dirigido de a hacia b, o decimos que el arco comienza en a y termina en b. En un grafo dirigido dado un vértice x, llamamos grado de entrada de x ge(x) a la cantidad de arcos dirigidos que comienzan en x, mientras que el grado de salida de x gs(x) es la cantidad de arcos dirigidos que terminan en x. En un grafo dirigido una secuencia de vértices (x0,x1,···,xl) es un camino si existen arcos dirigidos (xi,xi+1) para 0£ i<l.

Llamamos vista no dirigida de un grafo dirigido G=(V,A) al grafo no dirigido G'=(V,A') en el que tomamos los arcos dirigidos de G como arcos no dirigidos, i.e: A'={{x,y}:(x,y)Î A}.

Un grafo dirigido decorado G=(V,A,d) consta de un grafo (V,A) y una función d:A E que decora los arcos con elementos de cierto conjunto E de etiquetas (e.g E podría ser conjunto de números, en el caso de grafos cuyos arcos se decoran con cantidades --por ejemplo para representar distancia).

Árboles

Un grafo sin ciclos es un bosque o un grafo acíclico; mientras que un árbol es un bosque conexo.

TAD Árbol Binario

Llamamos árbol binario a un grafo dirigido decorado con etiquetas E={ Derecho, Izquierdo} que cumple: Un árbol binario tiene un vértice con grado de entrada 0 al que llamamos raíz. A los vértices con grado de salida 0 los llamamos hojas.

Para representar árboles binarios en un programa puede emplearse un TAD3 y con selectoras:

1.1.2   Lecturas recomendadas

Las definiciones de grafos son adaptadas de [6], mientras que el TAD Árbol Binario es adaptado de [11].

1.1.3   Ejercicios para afianzar teoría

  1. De un ejemplo de un grafo de orden 4 y tamaño 3 y dibuje una representación gráfica.
  2. En el grafo presentado al comienzo de esta guía ¿cuáles son los vértices adyacentes a c y cuales a b ?
  3. ¿Cual es el subgrafo inducido por V'={a} en el grafo de ejemplo?
  4. Los grafos G=({a,b,c},{{a,b},{a,c}}) y G'=({1,2,3},{{2,3},{3,1}}) son isomorfos, ¿Cual es la biyección (o correspondencia) entre sus vértices que preserva adyacencia?
  5. Presente dos grafos isomorfos de orden 4 y tamaño 3, junto con la biyección explicita.
  6. De un ejemplo de un grafo de orden 4, conexo, con al menos un ciclo de orden 3.

  7. De un ejemplo de un grafo 3-regular. Es su ejemplo un grafo regular?

1.1.4   Ejercicios de programación

  1. Implemente un TAD Árbol Binario y pruebe cada función con casos de diversa complejidad.

  2. Emplee el TAD que implementó en las siguientes funciones:
  3. Proponga un TAD grafo e impleméntelo.

  4. Usando su TAD escriba la función distancia que determine la distancia entre dos vértices de un grafo.

  5. Proponga un TAD grafo dirigido.
1
Note que la cardinalidad de un conjunto X, se denota por X, así que G= V(G).
2
Note que para determinar el tamaño de un grafo completo puede pensarse como formar todas las posibles parejas no ordenadas de vértices (hay ( 2n) posibles) o pueden tratarse de contar sin repetir: del primer vértice salen n-1 arcos, del segundo sin repetir serían n-2, del tercero sin repetir n-3 y así sucesivamente, del último vértice serían 0, de forma que el total de arcos sería 1+2+···+n+(n-1)=åi=1n-1i que a su vez es (n-1)(n) /2 que es igual a ( 2n).
3
TAD es abreviatura de Tipo Abstracto de Datos. Un tipo abstracto de datos encapsula un tipo con funciones al menos para construir elementos del tipo (i.e constructoras) y funciones para analizar o extraer información (i.e selectoras).

Capítulo 2   Árboles

2.1   Árboles de búsqueda

Indicadores de logro:

2.1.1   Teoría

Un problema importante en informática es determinar si un elemento e pertenece a una secuencia (e1, e2,· en) o a un conjunto {e1,··· en}. Aunque la solución más simple (examinar uno a uno los elementos de la secuencia o del conjunto) puede ser suficiente para algunos propósitos, cuando se requiere eficiencia deben emplearse estructuras de datos apropiadas.

En esta sección se estudian estructuras basadas en árboles que permiten efectuar búsquedas eficientemente.

Para medir eficiencia suelen emplearse dos métricas: espacio y tiempo. Ambas suelen medirse de forma asintótica para el peor de los casos. Por ejemplo con el algoritmo de búsqueda recién mencionado en el peor de los casos (si el elemento no está), se requieren n comparaciones cuando el tamaño del problema es n, se dice entonces que la complejidad temporal de ese algoritmo es O(n) (orden de n), como no se requiere espacio adicional para implementarlo su complejidad espacial es O(1).

Entonces al decir que la complejidad temporal de un algoritmo es O(f(n)) (siendo f(n) una función en la variable n), decimos que dada una entrada de tamaño n, el tiempo que requiere el algoritmo para dar una respuesta es proporcional a f(n). Al referirnos a complejidad espacial del orden O(f(n)) expresamos que la cantidad de espacio (i.e memoria) que un algoritmo requiere para completarse en el pero de los casos cuando procesa una entrada de tamaño n es proporcional a f(n).

Recorridos y otras operaciones con árboles binarios

Un árbol binario puede recorrerse de diversas formas, hay 3 de estas formas que se presentan a continuación junto como implementaciones en Ocaml que usan el siguiente TAD:1

type 'a arbin = ABvacio | ABcons of 'a arbin * 'a * 'a arbin;;

let izq= function
  | ABvacio -> failwith ("vacio")
  | ABcons (i,_,_) -> i
  ;;
let der=function
  | ABvacio -> failwith ("vacio")
  | ABcons (_,_,d) -> d
  ;;
let raiz= function  
  | ABvacio -> failwith ("vacio")
  | ABcons (_,r,_) -> r
  ;;
Note que los nombres de las funciones recuerdan el sitio donde se ubica la raíz.

Llamamos altura de un árbol a la cantidad de vértices del sendero más largo que exista en el árbol (téngase en cuenta que un árbol aquí se ha definido como un grafo dirigido, así que el sendero más largo debe partir de la raíz y terminar en una hoja). Para calcularla puede emplearse la siguiente función: 
let rec altura = function
        | ABvacio -> 0
        | ABcons(i,_,d) ->
                1 + (max (altura i) (altura d))
;;

Búsqueda en árboles binarios ordenados

Buscar un elemento en un árbol binario puede lograrse con más eficiencia si: En tal caso se habla de un árbol binario ordenado.



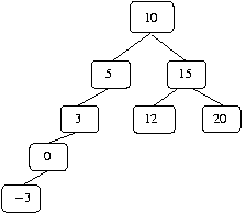
Figure 2.1: Ejemplo de árbol binario ordenado

Note que el árbol presentado en la figurar 2.1 es un árbol binario ordenado. Por ejemplo para buscar el 12 se requieren 3 comparaciones. Note además que un recorrido en inorden da la secuencia de elementos ordenada.

La implementación de este tipo en Ocaml puede hacerse con base en el mismo tipo arbin antes presentado3, pero ahora debe verificarse el siguiente invariante (no expresable como parte de la sentencia type): 
open Arbin;;
type 'a arbinord = 'a arbin;;
let rec inv = function
| ABvacio -> true
| ABcons(i,v,d) ->
        if (i<>ABvacio) then
                (v>(raiz i)) && (inv i)
        else
                true
        &&
        if (d<>ABvacio) then
                (v<=(raiz d)) && (inv i)
        else
                true
;;
El invariante expresado por esArbinord debe ser mantenido por funciones para insertar y eliminar, y puede ser aprovechado para efectuar búsquedas más rápidas para ciertos árboles.

Árboles AVL: binarios, ordenados y balanceados

Note que un árbol binario ordenado podría tener todos sus elementos en un sendero iniciado en la raíz y terminado en una única hoja, en tal caso buscar el menor elemento se realizará en tiempo proporcional al orden del árbol.

Para evitar situaciones como esta pueden agregarse condiciones al invariante de árbol binario ordenado, para mantener un árbol mejor distribuido, o en otras palabras un árbol balanceado: Si se logra mantener este invariante toda búsqueda se realizará con complejidad temporal O(log2 n) ---que es la complejidad temporal óptima para el problema de búsqueda.

Para lograr mantenerlo deben implementarse con atención las operaciones para insertar y eliminar elementos. Dado que estas operaciones deben mantener un invariante que requiere conocer altura de subárbol derecho e izquierdo, puede mantenerse esta información actualizada en los vértices del árbol (lo cual puede disminuir tiempo requerido para calcular la altura cuando se hace el balanceo, pero aumentar espacio empleado para mantener la información).



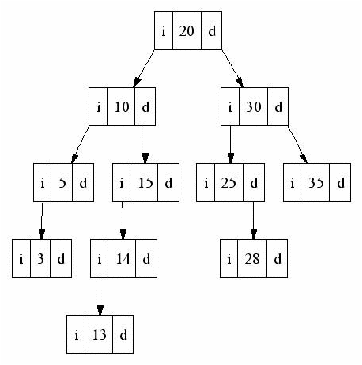
Figure 2.2: Ejemplo de árbol AVL

Una posibilidad es hacer el balanceo a medida que se inserta o elimina un nodo, otra opción es hacer una inserción o una eliminación como si el árbol fuera sólo un árbol binario ordenado y después balancear el árbol resultante. Para realizar tal balance (tras haber insertado o eliminado sólo un dato) pueden considerarse casos como los presentados en la figura 2.3 que permiten generalizar la solución.



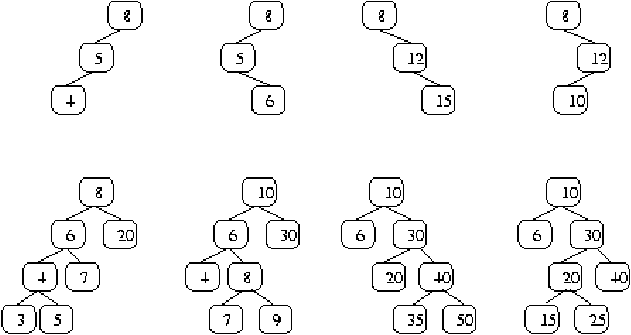
Figure 2.3: Ejemplo de casos para balancear

Por ejemplo puede balancearse el primer caso haciendo como una rotación a la derecha para obtener el grafo que tiene en su raíz el 5, como subárbol izquierdo la hoja con 8 y como subárbol izquierdo la hoja con 4.




2.1.2   Hacía la práctica


Visualizar un grafo (o un árbol) es un problema común, hay varias 
herramientas que ayudan entre las que se encuentra Graphviz que es 
multiplataforma, de libre redistribución y que puede usarse con 
bastante facilidad.



Graphviz se basa en un formato de texto plano (.dot) que especifica 
un grafo y en un lenguaje que facilita la presentación gráfica de
estos (lefty).



Entre las herramientas que ofrece este paquete están:
Por ejemplo el grafo presentado como ejemplo en la guía 1 (ver [ejem1]),
se escribió en un archivo ejem1.dot con el siguiente contenido:




digraph "ejemplo1" {

  graph [rankdir = "LR"];
  node [fontsize = "16" shape = "ellipse"];
  "a" 
  "b" 
  "c" 

  "a" -> "c" [dir="none"]
  "c" -> "b" [dir="none"]
}

Note que se comienza con digraph seguido del nombre
del grafo, después entre corchetes se agregan elementos los cuales
pueden ser:
En la implementación del TAD árbol binario que acompaña esta guía
se incluye una función 
dot_of_arbin: string -> ('a -> string) -> 'a arbin 
que permite generar un árbol binario en formato .dot.






2.1.3   Lecturas recomendadas


Desde el punto de vista de programación funcional, puede verse el uso 
de árboles de búsqueda en [5], desde el punto de vista
de programación imperativa en [11]. Puede consultase
más sobre Graphviz en [2].






2.1.4   Ejercicios para afianzar teoría



    

  1. 
 
Usando el tipo presentado al comienzo de esta guía puede escribirse
el árbol:
    

    
(ABcons(ABcons(ABvacio,3,ABvacio),2,
    ABcons(ABcons(ABvacio,3,ABvacio),5,ABvacio)))
    

    
Dibuje una representación gráfica de este árbol, escriba las listas que
resultan de recorrerlo en preorden, en inorden y en postorden.


  2.  
Algunos lenguajes de programación facilitan la creación de estructuras
polimórficas (en algunos contexto llamadas paramétricas o genéricas). 
Por ejemplo un TAD Árbol Binario Ordenado en Ocaml podría basarse en el 
tipo presentado al comienzo de esta guía.
    

    
Que podría después emplearse con enteros, cadenas o cualquier otro
tipo. Dado que Ocaml es un lenguaje con un recolector de basura, el
programador en casos sencillos no debe preocuparse por liberar memoria, 
detalle que puede ser difícil en lenguajes sin recolector de basura 
(y por tanto más eficientes en tiempo de ejecución) como C o C++. ¿Como 
podría implementar un árbol polimórfico en C? ¿Cómo puede implementar una
función para liberar memoria de una estructura como la que plantee?

    

    


  3.  
Hay diversas formas de implementar eliminación en un árbol binario ordenado,
explique (o implemente) por lo menos dos algoritmos para esto.

    

    


  4.  
Indique los árboles resultantes tras balancear los casos presentados
en la figura (2.3).

    

    


  5.  
Escriba en formato .dot el árbol 2.2 y visualicelo con
dotty.




2.1.5   Ejercicios de programación



    

  1. 
 
Implemente un TAD que representa un conjunto de enteros, empleando
una lista. Las operaciones mínimas que debe tener este TAD son:
    

    

    
Fije algunos casos de pruebas de diversa longitud (e.g 0, 10, 100, 10000) y
mida el tiempo que tarda la función ce_miembro al buscar un elemento
que no está en el conjunto (Ayuda: Para medir el tiempo que toma la 
ejecución de un programa --digamos prog-- puede emplear desde
la línea de comandos: time prog. Con este método diferenciará
hasta milésimas de segundo).
    

    
¿Cual es la complejidad de la función de búsqueda?

    

    


  2.  
Implemente el TAD del ejercicio anterior pero empleando una árbol
binario ordenado (Ayuda: puede emplear la implementación disponible
con estas guías en http://structio.sourceforge.net/guias/arbgraf/). 
Empleando los mismos casos de prueba del punto anterior
determine tiempo que tarda la función ce_miembro al buscar un elemento
que no está en el conjunto. ¿Cual es la complejidad de esa función con
esta implementación?

    

    


  3.  
Implemente el TAD del ejercicio anterior, excepto la función de
eliminar, pero empleando una árbol AVL . Realice pruebas análogas 
a las de los puntos anteriores e indique la complejidad de la función
ce_miembro.






2.2   Complejidad y Montículos

Indicadores de logro:



2.2.1   Teoría





 Cálculo de complejidad

Note que nuestra métrica de complejidad es independiente de multiplicación
por constantes, i.e para todo k¹ 0, O(f(n))=O(k· f(n)).
Así que O(1) es la mismo que O(5), mientras que O(n) es lo mismo 
que O(3n).



La complejidad temporal de una función puede determinarse contando cuantas
veces se realiza cierta operación básica escogida (por ejemplo
comparaciones o sumas o productos), en el peor de los casos cuando el 
tamaño de la entrada es n. 
Considere la función esta del TAD Árbol binario ordenado:

let rec esta e a=
        match a with
        | ABvacio -> false
        | ABcons(i,v,d) ->
                if v=e then
                        true
                else if (e<v) then
                        esta e i
                else
                        esta e d
;;

Las búsquedas más ineficientes ocurren cuando buscamos en un árbol 
nada balanceado de n elementos, los cuales están sobre un mismo 
camino de la raíz a una única hoja. En un árbol así podría buscarse
un elemento que no esté y podría requerirse recorrer todos los nodos
para decidirlo, de lo cual concluimos que la complejidad espacial
es orden de n i.e O(n). 



Para comprobarlo formalmente puede plantearse un conteo del número
de comparaciones realizadas en función del orden del árbol, tanto para 
el caso trivial como para otros casos en la peor de las situaciones:

C(0)=0


C(n)=2+C(n-1)

Note que se tiene una ecuación de recurrencia, para resolverla por
ejemplo puede:

    

  1. 
 Probar con algunos valores buscando encontrar un patrón que 
después debe comprobar


  2.  Dependiendo del tipo de ecuación, buscar y emplear un método de
solución apropiado (no para toda ecuación de recurrencia se conocen
fórmulas cerradas que la solucionen).


En este caso al probar con unos pocos valores de n puede sugerirse un 
patrón:







n
C(n)



0
0



1
2



2
4



3
6



:



n
2n





La solución propuesta puede comprobarse, verificando que satisface
la ecuación (i.e remplazando C(n)=2n en los 2 casos de la
ecuación de recurrencia):



Entonces la complejidad temporal será O(2n) que como se indicó antes
es lo mismo que O(n). 



Para determinar complejidad espacial puede emplearse un método análogo
que permita contar cuanto espacio se emplea en el pero de los casos.
Para el ejemplo de la función esta como no se emplea 
espacio adicional la complejidad espacial es O(1).



Para comparar, note que en un AVL la altura será de la forma 1+log2(n), 
como las búsquedas siempre recorren a lo sumo un camino de la raíz a una 
hoja, la complejidad temporal será O(log2 (n)).






 Montículos

En el caso de árboles AVL la complejidad temporal de una función 
para extraer el mínimo elemento es O(log2 (n)), en un montículo
la complejidad de esta operación es O(1), aunque la complejidad
de una búsqueda en un montículo es O(n) mientras que en un 
AVL es O(log2 n).



Así que un montículo es un tipo de árbol binario que privilegia
la operación de determinar el mínimo elemento. Para esto mantiene 
el siguiente invariante:

    

  1. 
 No hay elementos repetidos


  2.  Todo vértice es menor que sus hijos izquierdo y derecho


  3.  Es un árbol binario balanceado 


  4.  Todo subárbol es montículo

A continuación se anotan algunos detalles de las operaciones sobre
esta estructura:
La complejidad de las operaciones mencionadas es:







Función
Compl. temporal
Compl. Espacial



menor
O(1)
O(1)



esta
O(n)
O(1)



inserta
O(log2 (n))
O(1)



elimina
O(log2 (n))
O(1)







Table 2.1:  Complejidad de funciones sobre montículos.







2.2.2   Hacía la práctica





 El TAD conjunto de enteros

Como ya se ha experimentado es posible implementar el TAD
conjunto de enteros con las estructuras hasta ahora introducidas.



Sin embargo hay aplicaciones que requieren aún más eficiencia en
espacio y en las diversas operaciones. Si por ejemplo sólo se
usarán enteros entre 0 y 31 una posibilidad es representar un 
conjunto de estos enteros con un entero de 32 bits. El bit i-ésimo
en 1 indicaría que el número i-1 está en el conjunto. 



Por ejemplo el conjunto 0, 3, 8 se representa con el
entero (en binario) 100001001 que tiene en 1 las posiciones
(contando de derecha a izquierda) 1, 4 y 9.



Las diversas operaciones del TAD conjunto se implementan 
aprovechando operadores lógicos a nivel de bits. Por ejemplo
para determinar si un entero v es miembro de un conjunto,
puede hacerse la conjunción lógica entre el entero que
representa el conjunto y el entero que tiene el (v+1)-ésimo
bit en 1 y los demás en 0.



Esta idea es empleada por ejemplo en la implementación de conjuntos
del generador de compiladores PCCTS (ver [7]). Este puede 
soportar cualquier rango de enteros representando cada conjunto como una 
secuencia de enteros (y no como un sólo entero).






2.2.3   Lecturas recomendadas


Puede consultar más sobre montículos en
[5]. PCCTS es un generador de compiladores de
dominio público (antecesor de otro llamada Antares), puede ver más 
sobre este en [7].






2.2.4   Ejercicios para afianzar teoría



    

  1. 
 
Revise el TAD montículo en las implementaciones que acompañan estas guías,
calcule la complejidad de la inserción y justifique su respuesta.

    

    


  2.  
Haga tablas análogas a al tabla 2.1 que
indiquen complejidad de las diversas funciones de los TADs
árbol binario, árbol binario ordenado y AVL.

    

    


  3.  
Escriba los montículos que se obtienen tras insertar los
siguientes elementos a un montículo inicialmente vacío:
4, 3, 1, 2, 8, -6, 5

    

    


  4.  
Descargue las fuentes de PCCTS, revise la implementación de conjuntos
sobre bits de secuencias de enteros. La función set_deg 
retorna la cantidad de elementos de un conjunto. Revisando
esta función y el encabezado set.h descubra
que representa el campo n de la estructura set y
su relación con el campo setword.
    

    
Opcional: ¿Cómo podría implementarse la función set_deg sin usar el 
vector bitmaks en una plataforma de 32 bits?




2.2.5   Ejercicios de programación



    

  1. 
 
Pueden mezclarse de forma eficiente dos montículos (lo cual no es
fácil en el caso de árboles binarios ordenados). Implemente una
función mezcla: monticulo -> monticulo -> monticulo  que
mezcle dos montículos en un tercero y calcule la complejidad
temporal y espacial de su solución.


  2.  
Escriba una función que reciba un montículo y retorne una lista
con los elementos del montículo ordenados de menor a mayor.


  3.  
Escriba una función que reciba una lista de elementos (ordenables)
y que retorne un montículo con los mismos elementos. Calcule
la complejidad de la función que escribió. 
    

    
Note que esta operación junto con la función del punto anterior,
permiten ordenar una lista. Si esta operación se realiza de manera
eficiente se tendrá una implementación de un algoritmo conocido
como HeapSort.

    

    


  4.  
Usando las ideas presentadas en esta guía, implemente el TAD conjunto 
de enteros en el rango 0 a 31 con un entero de 32 bits (módulo Int32 en el 
caso de Ocaml). Implemente por lo menos las funciones sugeridas
en los ejercicios de la guía sobre árboles de búsquedas.






2.3   Árboles n-arios: árboles de sintaxis y árboles B

Indicadores de logro:



2.3.1   Teoría


En un árbol n-ario cada nodo puede tener un número variable
de subárboles, puede modelarse en Ocaml con un tipo como:




type 'a arbnario= ANvacio | ANcons of 'a * ('a arbnario) list;;

junto con un invariante para evitar representar con diversa sintaxis
el mismo árbol: El constructor ANvacio no aparece en
la lista de un constructor ANcons.






 Árboles de sintaxis abstracta

Un árbol de sintaxis abstracta permite representar ciertos elementos de un 
lenguaje para después analizarlo o transformarlo. Por ejemplo para un
lenguaje simple que permita realizar operaciones aritméticas basta
el siguiente árbol (note que algunos nodos son binarios, mientras que
otros unarios y otros sólo permiten representar hojas7):




type exprar = Const of int | InvAd of exprar | Suma of exprar * exprar | 
        Resta of exprar * exprar | Prod of exprar * exprar |
        Div of exprar * exprar;;

usándolo, la expresión 3*(-5+4) se representa como:




Prod(Const(3), Suma(InvAd(Const(5)),Const(4)))

Es posible hacer una función que reciba una cadena con la sintaxis
apropiada y genere un árbol de estos. A tal función se le llama un
reconocedor8 para el lenguaje.
De esta manera será fácil implementar funciones que empleen tales 
expresiones. 



El árbol de sintaxis para expresiones regulares del analizador léxico
ocamllex es9:




type regular_expression =
    Epsilon
  | Characters of char
  | Eof
  | Sequence of regular_expression * regular_expression
  | Alternative of regular_expression * regular_expression
  | Repetition of regular_expression
  | Bind of regular_expression * string

En este árbol se representan expresiones regulares como:
Un árbol de sintaxis para una porción del formato de graphviz puede
ser10:




(** Identificación de un nodo *)
type idNodo=string;;

(** Un arco puede conectar un nodo o un campo de un nodo registro *)
type arco_ext=Id_nodo of idNodo | Id_field of idNodo * string;;

(** Un atributo tiene una identificación y un valor. *)
type atributo=string*string ;;

(** Un arco tiene un nodo fuente, un destino y una lista de atributos *)
type arco=arco_ext*arco_ext*(atributo list);;

(** Un nodo tiene una identificación y una lista de atributos *)
type nodo=string*(atributo list);;

(** Un grafo tiene una identificación, una lista de nodos y una lista de arcos *)
type dot_graph=string*(nodo list*arco list);;

Incluso es posible proponer árboles de sintaxis para lenguajes naturales 
como el español o para porciones de este.



En general estos árboles no cumplen invariante alguno, aunque de una aplicación
a otra pueden imponerse invariantes por ejemplo para mejorar eficiencia.






 Árboles B

En diversas aplicaciones se requiere mantener en cada nodo del árbol
una llave junto con los datos que se desean representar. De esta forma 
el ordenamiento de los nodos puede hacerse con las llaves. Esta es una
situación típica en bases de datos, pues cada tabla debe tener una llave,
que facilita ubicar registros completos.



Por ejemplo el tipo árbol binario antes estudiado podría definirse y
usarse así:




 type ('a,'b) arbindat = ABDvacio | 
 ABDcons of (('a,'b) arbindat * ('a*'b) * ('a,'b) arbindat);;

let ej=ABDcons(ABDvacio,(10,"Magdalena"),ABDvacio);;

Note que el árbol polimórfico tiene dos parámetros: 'a que
será el tipo de la llave y 'b que será el tipo de los datos. En
el ejemplo presentado las llaves son enteras, mientras que los datos
mantenidos son cadenas.



Además de esto en una base de datos debe buscarse minimizar
las transferencias de bloques de datos de disco a memoria y viceversa.
En un árbol AVL el balanceo que debe hacerse después de insertar o
eliminar elementos puede requerir hacer varios intercambios en
el árbol (i.e varias transferencias en disco en el caso de una B.D). 
Para disminuir la posibilidad de balancear puede mantenerse más de 
un dato en cada nodo hasta un cierto máximo, así al insertar 
sólo debe balancearse si se crea un nuevo nodo cuando no haya espacio 
para más datos en otros nodos y al eliminarse sólo debe
balancearse cuando desaparezca un nodo después de que todos los datos
que tuviera hubieran sido eliminados.



Un árbol B es un árbol n-ario balanceado sin llaves repetidas,
que en cada nodo mantiene el siguiente invariante:
Una representación gráfica de un árbol B se presenta en la figura ??.











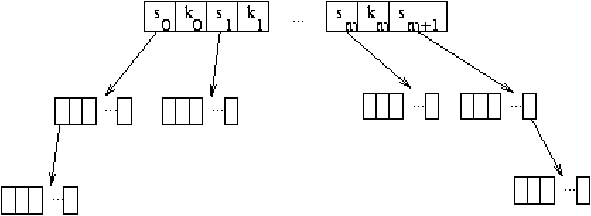
Figure 2.4: Ejemplo de árbol B genérico





La altura de un árbol B con n llaves es (é logm(n) ù).



Pueden verse estas ideas en la práctica en la base de datos con
fuentes de dominio público SQLite (ver [3]). 






2.3.2   Hacía la práctica





 Lineamientos de programación

Examinando las fuentes de SQLite (ver [3]) pueden inferirse los
siguientes lineamientos, que resultan útiles para cualquier
proyecto en C:






2.3.3   Lecturas recomendadas


Puede consultar más sobre árboles B y B+ en 
[8], y una descripción de inserción y eliminación en
árboles B en [1]. SQLite es un motor de bases de datos relacionales
implementado en C, es de dominio público, puede consultarse más en
[3].






2.3.4   Ejercicios para afianzar teoría



    

  1. 
 
Revise la implementación del TAD árbol n-ario que acompaña estas guías y
proponga una definición alterna para la función altura.

    

    


  2.  
En la documentación de Ocaml, revise la sintaxis de expresiones regulares que
acepta ocamllex, después escriba ejemplos de cadenas que correspondan
con cada una de las siguientes y una expresión que las represente usando
el árbol de sintaxis introducido en la guía:


    


  3.  
De un ejemplo del uso del árbol de sintaxis para el formato de Graphviz,
presentando la sintaxis concreta de su ejemplo y su representación usando
la estructura de datos dada.

    

    


  4.  
Consulte un algoritmo para inserción en un árbol B y de un
ejemplo.

    

    


  5.  
Obtenga las fuentes de SQLite y revise la implementación de la
función fileBtreeMoveto que busca una llave en un
árbol B. Descubra para que se usa el cursor pCur y el campo 
idx de tal cursor.
    

    




2.3.5   Ejercicios de programación



    

  1. 
 
Implemente las siguientes funciones para árboles n-arios:


    


  2.  
Haga funciones que muestren la representación como cadenas de cada
uno de los 3 árboles de sintaxis presentados como ejemplo.

    

    


  3.  
Describa un lenguaje de programación sencillo (o parte de un lenguaje) que 
conozca y proponga un árbol de sintaxis abstracta para este. Después
haga una función que a partir de un árbol de esto retorne una
representación como cadena.

    

    


  4.  
Proponga un tipo para un árbol B, e implemente una función que verifique
el invariante.
    

    
Opcional: Implemente una función de inserción.






1
 Disponible como arbin.ml entre
las implementaciones distribuidas con estas guías http://structio.sourceforge.net/guias/arbgraf/.


2
 Con propósitos 
prácticos, puede asociarse información a los vértices o a los arcos de un 
grafo.


3
 Este TAD
está disponible en las implementaciones que acompañan esta guía
en el módulo arbinord.ml


4
 Si se permiten vértices
repetidos junto con la convención de que estén en subárbol derecho,
no podrían balancearse muchos árboles con elementos repetidos. Si 
no se sigue convención alguna --i.e pueden haber repetidos a izquierda 
o derecha-- no podría aprovecharse que el árbol está ordenado en 
búsqueda de ocurrencias del elemento repetido.


5
 El formato PostScript es estándar
de varias impresoras laser, es apropiado para incluir en documentos de
TeX o LaTeX.


6
 La conversión de GIF a otros
formatos es fuertemente sugerida, pues GIF emplea un algoritmo de compresión
patentado por Unisys.


7
 Este
ejemplo es solución a un ejercicio de la sección ``Tipos definidos
por usuario'' de [10].


8
 Del inglés parser.


9
 Ver archivo lex/syntax.mli de la distribución
de fuentes de Ocaml 3.07


10
 El árbol presentado se basa en la implementación
de [9].






Capítulo 3   Grafos







3.1   Expresiones regulares y autómatas finitos

Indicadores de logro:



3.1.1   Teoría


Las expresiones regulares se emplean para describir una serie de
cadenas de manera concisa. Se han introducido en guías anteriores y 
son usadas por diversas herramientas 
(como grep, lex, sed, awk, perl),



Como caso de estudio del uso de grafos en esta guía presentamos
una forma de implementar un reconocedor de expresiones regulares usando 
autómatas finitos determinísticos.



Además de introducir definiciones formales, se estudian algoritmos que 
permiten:

    

  1. 
 transformar una expresión regular primero a un autómata finito no 
determinístico 


  2.  después transformar el autómata finito no determinístico a uno
determinístico eficiente.

 


 Lenguajes

Un lenguaje es un conjunto de cadenas sobre un alfabeto dado. Un
alfabeto es un conjunto finito de símbolos, una cadena es una secuencia
finita de tales símbolos.



Por ejemplo sobre el alfabeto S={0,2,5} un lenguaje posible
es L={000,205,5,5555 }.



La cadena vacía se denota e, el lenguaje {e} contiene
únicamente la cadena vacía.



Dados dos lenguajes A y B podemos definir algunas operaciones:
Un reconocedor para un lenguaje es un programa que dada una cadena s
decide si pertenece o no al lenguaje.






 Expresiones regulares

Una expresión regular denota un lenguaje1
En cuanto a sintaxis concreta, de estos operadores, * tiene precedencia 
máxima, mientras que | tendrá precedencia mínima, pueden emplearse 
paréntesis para cambiar la precedencia y como convención los caracteres
de escape \\, \*, \|, 
\( y \) denotarán los caracteres
\, *, |, ( y ) respectivamente.



En la sección sobre árboles de sintaxis se introdujo un tipo que
puede adaptarse (eliminando el constructor Eof) para representar
las expresiones regulares aquí presentadas.






 Autómatas Finitos

Un autómata finito es un grafo directo decorado2.
Se usa como reconocedor de lenguajes, los nodos representan posibles estados
durante el reconocimiento, y los arcos representan posibles transiciones de
un estado a otro. Hay un nodo inicial y un conjunto de nodos finales
(cuando se comienza el reconocimiento de un nuevo texto, el autómata
comienza en el estado inicial y la cadena pertenece al lenguaje si
alcanza un estado final cuando la cadena se procesa por completo).
Cada etiqueta tiene una letra que indica cuando puede ocurrir una
transición.







 





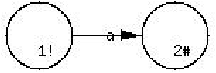
Figure 3.1: Ejemplo de autómata finito







 

En la figura 3.1, hay un arco del vértice 1 al vértice 2 con
etiqueta a. El nodo inicial es 1 que se indica por el símbolo !,
mientras que el nodo final es 2 que se indica por el símbolo #.



Si durante un reconocimiento el estado es 1, irá al estado 2 sólo si
el siguiente carácter del texto reconocido es a.



Hay dos clases de autómatas finitos: determinísticos (AFD) y 
no-determinísticos (AFN), las diferencias son:
Para efectos de implementación es más sencillo hacer un reconocedor con
un AFD, pues los cambios de estado se determinan con una sola comparación.






 De expresiones regulares a autómatas finitos eficientes

Es relativamente fácil generar un AFN que reconozca el lenguaje representado
por una expresión regular, basta aplicar las transformaciones de la
figura ??.







 





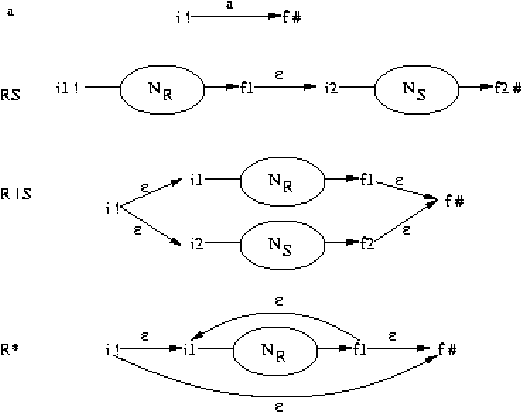
Figure 3.2: Transformaciones de expresiones regulares en autómatas finitos 
no determinísticos







 

Una característica de esta transformación es que da un AFN que tienen un
sólo estado final. En el primer caso, el de un símbolo, el estado inicial 
lo representamos con i mientras que el estado final con f.



Note que a representa un símbolo cualquiera del alfabeto, mientras
que R y S son expresiones regulares. Las elipses NR y NS
representan el autómata finito que resulta de transformar R y S
respectivamente, el primero tiene como estado inicial i1 y como
estado final f1, los análogos para NS son i2 y f2. 



Por ejemplo para transformar la expresión regular "(ab)|c*":
pueden crearse subgrafos siguiendo las reglas descritas hasta obtener
el grafo que corresponde a la expresión completa, como se presenta
en la figura ??.







 





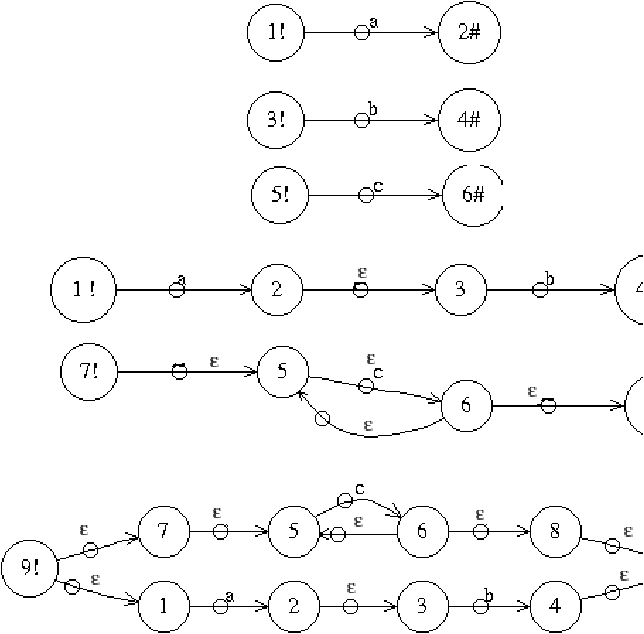
Figure 3.3: Ejemplo de transformación de la expresión (ab)|c*







 

Por facilidad y eficiencia al implementar un reconocedor de
lenguajes regulares puede resultar buena opción transformar el AFN 
que se obtiene tras traducir la expresión regular en un AFD mínimo, 
labor que puede hacer en dos pasos: (1) transformando el AFN en un AFD y 
(2) minimizando el número de estados del AFD.



Transformación de un AFN en un AFD



La idea es identificar muchos nodos de un AFN en un sólo nodo de un AFD. Todos los
vértices de un AFN a los que pueda llegarse desde un nodo dado pasando sólo
por arcos con etiqueta e deben identificarse como un único nodo en
el AFD (la clausura vacía de un conjunto de nodos N consta justamente 
de todos los nodos a los que puede llegarse desde nodos de N pasando sólo
por arcos con etiqueta e).



En el siguiente algoritmo D será el AFD que se construye, cada vértice de
D será un conjunto de nodos del AFN.




I=clausura\_epsilon(nodo inicial del AFN)
D=({I},{}) 
Si I contiene un nodo final marcarlo como vértice final de D
I no ha sido visitado
mientras (haya vértices no visitados en D)
        N=Tomar un vértice (conjunto) no visitado de D
        marcar N como visitado
        para cada etiqueta posible l 
                S=conjunto de nodos a los que se puede llegar desde
                  nodos en N pasando por arcos con etiqueta l
                T=clausura_epsilon(S)
                si (T ya es vértice de D) entonces
                        agregar en D un arco de N a T con etiqueta l
                sino
                        agregar T como vértice no marcado a D
                        si T contiene el vértice final del NFA marcar T como final
                        agregar un arco de N a T con etiqueta l
                fin-si
        fin-para
fin-mientras

Minimización de la cantidad de estados de un DFA 



Dados todos los estados de un DFA, la idea es hacer una partición P de
estos estados identificando en el mismo subconjunto todos los vértices que
tengan las mismas salidas (i.e todos ellos tienen arcos que
parten a los mismo subconjuntos con las mismas etiquetas).



Inicialmente divida los estados en dos grupos F y NF donde
F contiene todos los estados finales y
NF los estados no finales, P={F,NF}. 




mientras (se haya modificado P)
  para cada posible etiqueta c del DFA inicial
    para cada conjunto S de P
      escoja un elemento x de S del que salga un arco con etiqueta c
      S1={y en S | y va al mismo conjunto de P que x por una etiqueta c}
      S2=S-S1
      eliminar S de P
      agregar S1 a P
      si S2 no es vacío agregar S2 a P
    fin-para
  fin-para
fin-mientras








3.1.2   Lecturas recomendadas


La fuente de consulta fundamental ha sido 
[4], libro clásico y muy recomendado.






3.1.3   Ejercicios para afianzar teoría



    

  1. 
 
Sobre un alfabeto S={x,y,7,2}, se definen los lenguajes
A={xx, xy, x72} y B={xi | iÎ Nat} donde
x0=e, x1=x, x2=xx, x3=xxx y así sucesivamente.
¿A qué lenguaje corresponden: A.A, A3, AÈ A3, A*,
AÈ B, B2, (AÈ B)*.

    

    


  2.  
¿Qué lenguajes representan las siguientes expresiones regulares

    

    

    


  3.  
Escriba AFNs o AFDs que reconozcan cada uno de los lenguajes descritos
por las expresiones regulares del punto anterior.

    

    


  4.  

    

    
 

    

    

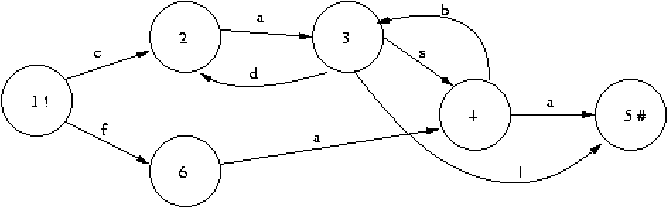
    Figure 3.4: AFD

    



    

     
    
Dado el AFD de la figura 3.4 indique cuales de las siguientes cadenas
reconoce:

    


  5.  
Transforme cada una de las siguientes expresiones regulares a un
AFN siguiendo el algoritmo descrito en la guía, después transforme
el AFN resultante en un AFD siguiendo el algoritmo descrito en la guía.

    

    

    


  6.  
Minimice los estados de cada uno de los AFDs del ejercicio anterior, 
siguiendo el algoritmo descrito en la guía.




3.1.4   Ejercicios de programación



    

  1. 
 
Empleando el tipo

    type expreg=
        Epsilon
        | Car of char
        | Secuencia of expreg * expreg
        | Alternativa of expreg * expreg
        | Repeticion of expreg
;;

    (adaptado de uno introducido en la guía anterior) escriba la función
reconoce_expreg: int -> int -> string -> expreg que recibe como 
tercer parámetro una cadena con una expresión regular (con la sintaxis
concreta descrita en esta guía), como primer parámetro una posición
inicial dentro de la cadena y como segundo parámetro una posición final
dentro de la cadena. Retorna la expresión regular que puede
reconocer entre las posiciones inicial y final (incluidas).

    

    


  2.  
Implemente un tipo paramétrico ('a,'b) afd para representar AFDs 
con nodos tipo 'a y etiquetas tipo 'b, e implemente la función
afd_reconocedor: string -> afd -> bool que retorne verdadero
sólo si el autómata reconoce la cadena que recibe.

    

    


  3.  
Para representar autómatas finitos no determinísticos con un sólo estado
inicial y un sólo estado final podría emplearse el tipo:
type ('a,'b) afn='a list * ('a*'a*'b option) list * 'a option * 'a option;;
    

    
La primera lista es de vértices, la segunda de arcos etiquetados, el tercer
elemento de la tupla es el vértice inicial y el último el vértice final. 
La etiqueta e se representa con None. El NFA vacio sería
([],[],None,None), los demás NFAs deben tener nodo inicial y final diferentes
a None (i.e Some x).
    

    
Usando este tipo (o uno análogo en un lenguaje diferente a Ocaml) y el
tipo expreg del primer ejercicio de esta guía, implemente la función
afn_de_expreg : int -> expreg -> ((int,char) afn, int) que
traduce una expresión regular a un AFN con el algoritmo descrito en la
guía. Los vértices los numera con enteros comenzando con el entero que
recibe como segundo parámetro. Retorna el AFN y el siguiente entero que
no se uso para numerar vértices.
    

    
Opcional: Los AFN que resultan del algoritmo de traducción descrito 
tienen una característica que puede aprovecharse para hacer una estructura
de datos más eficiente. De todo vértice salen a lo sumo dos arcos y
cuando salen dos ambos tienen etiquetas e.
Proponga una estructura de datos que aproveche esta característica e indique
que cambios deben hacerse a afn_de_expreg para que
la use.

    

    


  4.  
Empleando el tipo del ejercicio anterior, un tipo para AFDs ('a, 'b) afd,
y un TAD conjunto de enteros conjent, 
implemente la función 
afd_de_afn: (int, char) afn -> (conjent, char) afd 
que transforme un AFN en un AFD con el algoritmo descrito 
en la guía. 
    

    
Opcional: La eficiencia de esta transformación depende en buena
medida del TAD conjunto de enteros que se emplee. Mejore la
implementación de conjunto de enteros como bits en enteros de 32 bits,
para que emplee un vector de enteros en lugar de un sólo entero, y
verifique que funciona con la función de este ejercicio.

    

    


  5.  
Escriba una función que renombre los estados de un AFD para que sean
enteros: numest_afd: ('a, 'b) afd -> (int, 'b) afd. ¿Cuál es
la complejidad de esta función?

    

    


  6.  
Escriba una función que implemente el algoritmo de minimización de estados
de un AFD descrito en la guía:
minest_afd: (int, char) afd -> (conjent, char) afd.






1
 Los lenguajes que una
expresión regular puede denotar se llaman lenguajes regulares.


2
 Un grafo es decorado 
si a cada arco se le asocia un valor. Es decir
un grafo dirigido decorado con valores en un conjunto D, es una tupla 
G=(V,A,ea) donde V es conjunto de vértices, A es conjunto de arcos 
(parejas ordenadas de vértices) y ea:A D. Gráficamente
puede representarse agregando sobre cada arco el valor asociado.






Bibliografía




[1]

B-tree algorithms.
http://www.semaphorecorp.com/btp/algo.html, 2004.





[2]

Graphviz - open source graph drawing software.
http://www.research.att.com/sw/tools/graphviz/, 2004.





[3]

Sqlite: An enbeddable sql database engine.
http://www.sqlite.org/, 2004.





[4]

Alfred V. Aho and Jeffrey D. Ullman.
Principles of Compiler Design.
Addison Wesley, 1978.





[5]

Richard Bird.
Introducción a la Programación Funcional con Haskell.
Prentice Hall, 2000.





[6]

Béla Boolobás.
Graph Theory: An Introductory Course.
Springer Verlag, 1979.





[7]

Tom Moog.
Pccts resources.
http://www.polhode.com/pccts.html, 2004.





[8]

John Morris.
Data structures and algorithms.
http://ciips.ee.uwa.edu.au/ morris/Year2/PLDS210/ds_ToC.html, 2004.





[9]

Vladimir Támara Patiño.
Restricted design spaces: Visualization and consistency tools.
Technical Report 03/01, Sonderforschungsbereich 501, Teilprojekt B5,
 Universität Kaiserslautern,
 "http://www-madlener.informatik.uni-kl.de/ag-madlener/publications/2001/sfb501-03-01.ps.gz", 2001.





[10]

Vladimir Támara and Carlos Fidel Rodriguez.
Programación en ocaml.
http://structio.sourceforge.net/guias/arbgraf, 2004.





[11]

Jorge Villalobos, Alejandro Quintero, and Mario Otero.
Estructuras de Datos: Un Enfoque desde Tipos Abstractos.
Mc-Graw Hill. Ediciones Uniandes, 1988.





Index








This document was translated from LATEX by
HEVEA.