

-
LOGRO: Plantea problemas de programación lineal
- LOGRO: Resulevel problemas de programación lineal con el método simplex y puede explicar este método
1.1 Introducción a optimización y programación lineal
Indicadores de logro:
-
INDICADOR: Plantea programas lineales
- INDICADOR: Grafica regiones factibles que restringen un programa lineal
Un problema de optimización es de la forma:
| minimizar o maximizar |
f(x) |
| sujeto a |
x∈Ω |
Cuando la función por minimizar/maximizar (i.e la función objetivo) es
lineal y el conjunto Ω se puede expresar con igualdades o
desigualdades lineales (con ≥ y ≤) se trata de un problema de
programación lineal.
Todo problema de programación lineal puede traducirse a un forma estándar:
| minimizar |
|
| sujeto a |
Ax=b |
| |
x≥ 0 |
teniendo en cuenta que la notación u≥v con u=
(u1, ... un) y v=(v1, …, vn)
indica ui≥ vi (para i=1,2... n).
Para transformar problemas de programación lineal a la forma estándar
pueden emplearse estas técnicas:
-
Una desigualdad Σi=1najixi≤ Mj puede convertirse
en igualdad introduciendo una nueva variable de holgura
Σi=1najixi + yj = Mj con yj≥ 0.
- De forma análoga Σi=1najixi ≥ mj puede convertirse
en igualdad con una nueva variable excedente yj≥ 0 para dar
Σi=1najixi − yj = mj.
- Sustituir una variable no acotada xi con dos variables nuevas ui>0 y
vi>0 siendo xi=ui−vi. Otra posibilidad es emplear alguna igualdad
para obtener una expresión para xi en función de las demás variables y
sustituir tal expresión en las demás ecuaciones con lo que se obtiene
un sistema de m−1× n−1.
- Dado que max Σj=1ncjxj = − min Σj=1n−cjxj, pueden
convertirse problemas de minimización en maximización y viceversa, remplazando
la función objetivo (por ejemplo si la función objetivo es
maxcTx se remplaza por min−cTx.)
También puede llevarse el problema a una forma canónica de
minimización/maximización:
| minimizar |
|
| sujeto a |
Ax≥ b |
| |
x≥ 0 |
o
| maximizar |
|
| sujeto a |
Ax≤ b |
| |
x≥ 0 |
Los puntos que cumplen las restricciones se llaman soluciones factibles,
conforman una región limitada por los hiperplanos que cada una
de las restricciones representa al plantearlas como igualdades.
Algunos problemas que típicamente pueden expresarse como problemas de
programación lineal son:
-
Problemas de dieta o de mezcla de alimentos
- Problemas de almacenamiento
- Programación de producción (discretizando)
- Problemas de transporte
1.1.2 Lecturas recomendadas
Capítulo 1 (Introducción) de [4].
Capítulo 1 de [6].
Pueden consultarse diversas herramientas de fuentes abiertas y
comerciales para resolver problemas de programación lineal en
[1].
Algunos casos de éxitos en el contexto de empresas que han logrado
grandes ahorros por el uso de programación lineal pueden consultarse
en la introducción de [7].
1.1.3 Ejercicios
-
(Ejercicio 2 de [6]) Un fabricante desea producir una aleación
cuya composición, por peso, es 30% de metal A y 70% de metal B. Se dispone
de cinco aleaciones a los precios que se indican a continuación:
| Aleación |
1 |
2 |
3 |
4 |
5 |
| % A |
10 |
25 |
50 |
75 |
95 |
| % B |
90 |
75 |
50 |
25 |
5 |
| Precio/lb |
5$ |
4$ |
3$ |
2$ |
1.50$ |
La aleación deseada se conseguirá combinando algunas de las otras aleaciones.
El fabricante desea hallar las cantidades de las distintas aleaciones
necesarias y la combinación más barata. Formúlese este problema como un
programa lineal.
-
(Ejercicio 6 de [6]). Una gran compañia textil tiene dos plantas
de producción, dos orígenes de materias primas y tres centros
de entrega. El costo de transporte entre los orígenes y las plantas y entre las
plantas y los mercados es el siguiente:
| |
Planta A |
Planta B |
| Orígen 1 |
1$/ton |
1.50$/ton |
| Orígen 2 |
2$/ton |
1.50$/ton |
| |
Mercado 1 |
Mercado 2 |
Mercado 3 |
| Planta A |
4$/ton |
2$/ton |
1$/ton |
| Planta B |
3$/ton |
4$/ton |
2$/ton |
Se dispone de 10 toneladas del origen 1 y de 15 toneladas del origen 2. Los
tres centros de ventas necesitan 8 toneladas, 14 toneladas y 3 toneladas.
La capacidad de procesamiento de las plantas es ilimitada.
-
Formule el problema de encontrar la forma de envío de los
orígenes a las plantas y a los mercados que minimice el costo total de
transporte.
- Redúzca el problema a un solo problema estándar de trasnporte
con dos orígenes y tres destinos. (Sugerencia. Hálle las trayectorias de
costo mínimo de los orígenes a los mercados.)
-
(Ejercicio 1.8 de [6]) Convierta el siguiente problema a un
programa lineal en forma estándar:
| minimizar |
|x|+|y|+|z| |
| sujeto a |
x+y≤ 1 |
| |
2x+z=3 |
-
(Parte del ejercicio 1.3 de [4]) Considere el problema de ubicar
una nueva
máquina en un sistema existente que consiste de 4 máquinas. Estas máquinas
se localizan en las siguientes coordenadadas x1 y x2:
(3,0), (0,−3), (−2, 1), (1, 4). Suponga que las coordenadas de la
nueva máquina son (x1, x2). Formule como problema de programación
lineal, minimizar la suma de las distancias desde la nueva máquina a las
cuatro máquinas existentes. Use la “distancia en calles”; por ejemplo, la
distancia de (x1, x2) a la primera máquina localizada en (3,0)
es |x1−3|−|x2|.
-
(Tomado de [6]) Grafique la región factible (i.e de soluciones
factibles) del siguiente problema de programación lineal y después encuentre
la solución.
| maximizar |
x1 + x2 |
| sujeto a |
|
| |
x1+x2≤ 2 |
| |
2x1 ≤ 3 |
| |
x1≥ 0, x2≥ 0 |
1.2 Método Simplex
Indicadores de logro:
-
INDICADOR: Revisa fundamentos teóricos del método Simplex
- INDICADOR: Resuelve algunos problemas de programación lineal usando el método simplex
Posibilidades con respecto a la región factible y la solución
En algunos casos puede considerarse una representación gráfica del
problema de programación lineal. Por ejemplo con el problema:
| min |
−x1−3x2 |
| sujeto a |
x1+x2≤ 6 |
| |
−x1+2x2≤ 8 |
| |
x1≥ 0, x2≥ 0 |
La región de soluciones factibles está limitada por las rectas:
que se presentan en la figura 1.1.
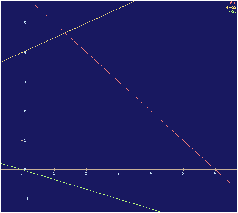
Figure 1.1: Región de soluciones factibles
En la misma gráfica se muestra una de las curvas de la función objetivo,
la que corresponde a −x1−3x2=z con z=0. Note que a medida que la
función objetivo
toma menores valores la recta correspondiente se desplaza hacia el nororiente.
Así que el valor mínimo (es decir el que alcanza la función objetivo para
cierto valor de z mínimmo pero cuya curva tiene al menos un punto
en común con la región factible) se alcanzará en el punto de intersección
de las rectas x2=6−x1 y x2=4+x1 /2, que es (4/3,
14/3).
En este caso hay una solución única y se trata de un punto extremo
de la región factible.
Si en el problema de programación lineal anterior se elimina la restricción
x1+x2≤ 6, la región factible es no acotada, y en este caso particular
todo valor negativo de z en z=−x1−3x2 dará lugar a una recta que se
intersteca con la región factible, de manera que la solución óptima no
está acotada. Sin embargo, es posible que una región factible sea no acotada
y exista un optimo finito, por ejemplo si en el problema
descrito en este parráfo se cambia la función objetivo por
max−x1−3x2 (cuya solución es (0,0) que también es punto extremo de
la región factible).
Al considerar el problema
| min |
−x1−x2 |
| sujeto a |
x1+x2≤ 6 |
| |
−x1+2x2≤ 8 |
| |
x1≥ 0, x2≥ 0 |
Notamos que la pendiente de la función objetivo para todo valor de z
en z=−x1−x2 es -1 al igual que la pendiente de x1+x2=6, por esto
resultará toda una familia de soluciones óptimas, i.e las que
cumplen −6=−x1−x2, y en particular los puntos extremos
(6,0), (4/3, 14/3).
Otra posibilidad que puede tenerse es una región factible vacía, por
ejemplo agregando al problema anterior la restricción x2≥ 8.
Observaciones generalizables
De los ejemplos anteriores puede generalizarse: Cuando hay solución
óptima está en un punto extremo.
Note que al convertir el problema en forma estándar se introducen nuevas
variables y que las rectas que limitan la región factible se obtienen igualando
las diversas variables a cero. Retomando el ejemplo inicial de esta guía:
| min |
−x1−3x2 |
| sujeto a |
x1+x2+s1 =6 |
| |
−x1+2x2 + s2 = 8 |
| |
x1≥ 0, x2≥ 0, s1≥ 0, s2≥ 0 |
Al tomar s1=0 se tiene la recta x1+x2=6, la recta −x1+2x2=8 se
logra tomando s2=0 y justamente el punto optimo corresponde a
la solución del sistema de 2 ecuaciones y 2 incognitas que resulta
cuando s1=0 y s2=0. Esta característica también es generalizable
tras introducir el concepto de solución básica.
Definición 1
Dadas m ecuaciones lineales en n incongnitas, de la forma
Ax=b y B submatriz de m× m no singular con
columnas de A. Si todas las n−m columnas de x no
asociadas a columnas de B son igales a 0, llamamos
variables básicas a las variables asociadas a B
(i.e xB) y a una solución al
sistema que también cumpla Bxb=b se le llama
solución básica respecto a la base B.
De aquí en adelante supondremos que A es de rango completo, es decir
que las m filas de la matriz A son linealmente independientes.
Definición 2
Si una o más variables de una solución básica son 0, se
trata de una solución básica degenerada.
Definición 3
Dado el sistema
si x lo satisface decimos que x es
solución factible
, si además es básica decimos que es
solución básica factible
. Con respecto al problema
| minimizar |
cTx |
| sujeto a |
Ax=b |
| |
x≥ 0
|
solución factible
óptima
, si además x es solución básica decimos que es
solución factible óptima básica
.
Teorema 1
(Teo. Fundamental de la programación lineal)
-
Si hay una solución factible, hay una solución
básica factible.
- Si hay una solución factible óptima, hay una
solución factible óptima básica.
Método Simplex
Como la solución óptima (de existir) debe ser una solución básica,
basta considerar las soluciones básicas (que son
n m). El método simplex hace justamente esto, pero
evitando soluciones no factibles y procurando mejorar la función objetivo
con la elección de las variables básicas.
Lo introducimos con un ejemplo tomado de [9]:
| maximizar |
5x1+4x2 |
| sujeto a |
6x1+4x2≤ 24 |
| |
x1+2x2≤ 6 |
| |
−x1+x2≤ 1 |
| |
−x2 ≤ 2 |
| |
x≥ 0
|
Una vez expresado el problema en forma estándar podemos formar una
tabla como
donde r es un vector que ayuda a
escoger la próxima variable básica para tratar de disminuir más
la función objetivo y z es el valor de la función objetivo.
El ejemplo en forma estándar es:
| min |
−5x1−4x2 |
| sujeto a |
6x1+4x2+s1 = 24 |
| |
x1+2x2 +s2 = 6 |
| |
−x1+x2 +s3 = 1 |
| |
−x2 + s4 = 2 |
| |
(x,s)≥ 0
|
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝ |
| 6 |
4 |
1 |
0 |
0 |
0 |
24 |
| 1 |
2 |
0 |
1 |
0 |
0 |
6 |
| −1 |
1 |
0 |
0 |
1 |
0 |
1 |
| 0 |
−1 |
0 |
0 |
0 |
1 |
2 |
| −5 |
−4 |
0 |
0 |
0 |
0 |
0 |
| |
|
|
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠ |
La submatriz de A que resulta ser la matriz identidad de
m× m determina cuales son las variables básicas. En
este ejemplo son (s1, s2, s3, s4). Como las variables
no básicas son x1 y x2 su valor es cero y por esto el
valor de la función objetivo inicialmente es z=0.
Note que en este caso el vector r comenzó como los coeficientes de
la función objetivo en cada una de las variables1
El método simplex provee un mecanismo para determinar que
variable vale la pena agregar como básica y cual de las
básicas sacar. La variable que pasa a ser básica es la variable
no básica que tenga en la columna que le corresponde el menor
rj negativo. Suponiendo que se hará básica la j-esima
variable, la variable que deja de ser básica se determina
escogiendo la que asociada a
siendo xi el valor de la última columna en la fila i, y
aij el valor que está en la columna j (la de la variable
que entrará) y fila i.
Para el ejemplo presentado se ingresará x1 a la base de
básicas (pues aporta un peso de -5 para disminuir la función
objetivo), y se sacará s1 porque 24 /6 es el valor
mínimo de entre 24/6 y 6/2 .
Para que la matriz identidad ahora incluya la primera columna
y tenga el uno en esa columna en la primera fila, aplicamos un
paso de la reducción de Gauss-Jordan usando como pivote el
6 que está en la primera columna y primera fila, para obtener:
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝ |
| 1 |
|
|
0 |
0 |
0 |
4 |
| 0 |
|
|
1 |
0 |
0 |
2 |
| 0 |
|
|
0 |
1 |
0 |
5 |
| 0 |
1 |
0 |
0 |
0 |
1 |
2 |
| 0 |
|
|
0 |
0 |
0 |
20 |
| |
|
|
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠ |
la cual indica que al escoger como básicas las variables
(x1, s2, s3, s4) se obtiene la solución
(x1, x2, s1, s2, s3, s4)=(4, 0, 0, 2, 5, 2) que logra
un valor de la función objetivo de −20.
Tras analizar la nueva tabla puede concluirse que el nuevo
pivote debe ser la celda de la segunda columna y segunda fila
(donde está el valor 4/3), que corresponde a incluir
entre las básicas a x2 y sacar de las que hay a s2.
Tras reducir se obtiene:
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝ |
| 1 |
0 |
|
|
0 |
0 |
3 |
| 0 |
1 |
|
|
0 |
0 |
|
| 0 |
0 |
|
|
1 |
0 |
|
| 0 |
0 |
|
|
0 |
1 |
|
| 0 |
0 |
|
|
0 |
0 |
21 |
| |
|
|
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠ |
que da la respuesta óptima (pues ya no hay coeficientes negativos
en la fila r) que es:
(x1,x2,s1,s2,s3,s4)=(3, 3/2, 0, 0, 5/2,
1/2) que hace que la función objetivo alcance
el valor −21.
Un resumen, presentado en [9] de los pasos por
emplear cuando no hay soluciones básicas degeneradas es:
-
Determinar una solución básica factible de inicio
- Seleccionar una variable de entrada aplicando
la condición de optimalidad. Detenerse si no hay
variable de entrada; la última solución es la
óptima.
- Seleccionar una variable de salida aplicando la
condición de factibilidad.
- Determinar la nueva solución básica con los cálculos
adecuados de Gauss Jordan. Ir al paso 2.
Teniendo en cuenta:
-
Condición de optimalidad: La variable de entrada es
la que tenga el menor coeficiente negativo en la
columna r. Los empates se rompen de
forma arbitraria. Se llega al óptimo cuando todos
los coeficines de variables no básicas son no
negativos.
- Condición de factibilidad. La variable de salida es
la asociada a la mínima razón no negativa.
Los empates se rompen de forma arbitraria.
1.2.2 Lecturas recomendadas
Capítulo 1 (Introducción) de [4].
El teorema fundamental de programación lineal se presenta y
demuestra en [6].
1.2.3 Ejercicios
-
Con respecto al planteamiento geométrico/gráfico de un problema de
programación lineal, determine la dirección en la que deben moverse
las curvas de la función objetivo para maximizarla o minimizarla
(Ayuda: use el gradiente).
-
Para el primer ejemplo introducido en esta guía, presente todas las
submatrices de m× m de A y determine la solución básica
asociada a cada una de ellas, indicando cuales son factibles.
-
Emplee el método simplex para solucionar el ejercicio de la aleación
planteado en la guía 1.
-
(Ejercicio 3.3.2.11 de [9]) Gutchi Company fabrica bolsos de mano,
bolsos para rasuradoras y mochilas. En las tres fabricaciones se usa piel y
material sintético, pero la piel parece ser la materia prima limitante
principal. En el proceso de producción intervienen dos clases de mano de
obra especializada: costura y acabado. La tabla siguiente muestra la
disponibilidad de los recursos, sus consumos por los tres productos y las
utilidades por unidad.
| Recurso |
Bolso |
Bolso para |
Mochila |
Disponibilidad |
| |
de mano |
rasuradora |
|
diaria |
| Piel (pie2) |
2 |
1 |
3 |
42 pies2 |
| Costura (hr) |
2 |
1 |
2 |
40 hr |
| Acabado (hr) |
1 |
0.5 |
1 |
45 hr |
| Precio venta ($) |
24 |
22 |
45 |
|
| |
Formule el problema como programa lineal y resuélvalo.
-
Consulte el artículo “Linear Programming The Story about How It Began”
de Dantzig, disponible en
http://cursos.itam.mx/licenciatura/jmorales/public_html/PDFfiles/dantzig.pdf y escriba un resumen corto. (Aclaración: Vladimir Támara no
está de acuerdo con investigar o apoyar sistemas de defensa que no
respeten la vida).
-
Demuestre que el conjunto de direcciones de la región factible
de un problema de programación lineal es convexo.
1.3 Método Simplex
Indicadores de logro:
-
INDICADOR: Hace un paralelo entre solución geométrica y algebráica a un problema de programación líneal
- INDICADOR: Explica las reglas del método simplex y puede emplear el método de las dos fases
Interpretación geométrica
Definición 1
Un conjunto C en Rn es convexo si para todo par
x1,x2∈ C y todo número real α, 0<α<1
el punto αx1+(1−α)x2 también
está en C.
Definición 2
Un punto x de un conjunto convexo C se denomian
punto extremo de C si no hay 2 puntos distintos
x1 y x2 en C tales que
x=αx1+(1−α)x2 para algún
α, 0<α <1.
Por ejemplo el conjunto de soluciones factibles de un problema de
programación líneal es convexo.
Teorema 1
(Equivalencia entre puntos extremos y soluciones básicas)
Sea A matriz de m× n de rango m, y
b un m-vector. Sea K politopo convexo formado
por los n-vectores que satisfacen:
Un vector x es punto extremo de K si y sólo si, x
es solución factible básica de Ax=b, x≥ 0.
Definición 3
Un conjunto C⊆ Rm es acotado si existe k∈ R tal que
para todo x∈ C, se da ||x||≤ k.
Definición 4
Un rayo es un conjunto {x+λd :λ≥ 0}
con d distinto de 0. Decimos que x es vertice del
rayo y d es su dirección.
Definición 5
Un vector d es dirección de un conjunto convexo C, si
para cualquier punto x∈ C el rayo con vertice en x
y dirección d está enteramente contenido en C, i.e
{x+λd :λ≥ 0}⊆ C
Ejemplo: Un conjunto acotado no tiene direcciones.
Ejemplo: Sea C={x : Ax=b, x≥ 0}. Un vector
d distinto de 0 es dirección si y solo si Ad=0 y
d≥ 0.
Ejemplo: En el caso C={x : Ax≥ b, x≥ 0}. Un
vector d es dirección si y solo si
Ad≥ 0 y d≥ 0 y d≠ 0.
Definición 6
Una dirección extrema de un conjunto convexo C es
una dirección del conjunto que no se puede representar como
combinación lineal positiva de dos direcciones distintas del conjunto.
Definición 7
d1 es no equivalente a d2 si no es
múltiplo positivo.
Teorema 2
Si la región factible es no vacía, existe una solución optima
finita si y solo si, cTdj≥ 0 para
cada j=1... l en donde d1, d2, ... dl
son las direcciones extremas de la región factible. En caso
contrario, la solución optima es no acotada.
Teorema 3
(Teorema de representación)
Sea C={x : Ax=b, x≥ 0} conjunto no vacío
con puntos extremos E={x1,...,xk} y direcciones
extremas D={d1,...,dl}:
-
D es vacío si y sólo si C es acotado
- x∈ C si y sólo si x puede representarse como
combinación convexa de los puntos extremos más una combinación
lineal no negativa de las direcciones extremas, i.e existen
λ1,...,λk≥ 0 y μ1,...,μl≥ 0
tales que λ1+...+λk=1 y
Inicio del método Simplex
Para iniciar el método simplex es indispensable que la tabla presentada
en la guía anterior incluya una matriz identidad. Para lograrlo podría
intentarse dividir la matriz A en básicas y no básica (digamos que
las básicas son las primeras): A=[B,D] lo que conlleva a una división
natural en las variables x=(xB,xD) y los
coeficientes de la función objetivo cT=(cBT, cDT)
y a un reformulación del problema en forma estándar:
| min |
cBTxB+cDTxD |
| sujeto a |
BxB + DxD=b |
| |
x≥ 0 |
La tabla simplex sería:
o
que podría incluir la matriz identidad y quedar lista para iniciar el método
simplex si premultiplicamos las primeras filas por B−1:
y después a la última fila le restamos cBT veces las anteriores:
| I |
B−1D |
B−1b |
| 0 |
cDT−cBTB−1D |
−B−1b |
Este procedimiento asegura que comenzariamos con una solución básica,
pero no asegura que sea factible pues algunos de los coeficientes
B−1b podrían ser negativos.
Una manera que asegura encontrar una solución básica factible para iniciar
el procedimiento simplex se conoce como el método de las dos fases.
La ídea es econtrar primero una solución al sistema
Método de las dos fases
Para encontrar una solución básica factible a
Ax=b con x≥ 0 pueden introducirse suficientes variables
artificiales2
y plantear el siguiente problema de programación lineal:
| min |
|
| sujeto a |
[A,I]x y=b |
| |
x≥ 0, y≥ 0 |
Resolver este problema corresponde a la primera fase del problema original.
Si la solución de este problema incluye y=0 tendremos
una solución básica factible con la cual iniciar el procedimiento simplex
del problema original (i.e con la cual iniciar la segunda fase). Si en la
solución resulta y≠ 0 sabemos que el problema original no tiene
siquiera una solución básica fáctible y menos una optima.
Revisando método simplex
Para escoger la variable que ingresa al conjunto de básicas, puede
considerarse la forma como mejoraría la función objetivo. Para esto
vale la pena expresar la función objetivo sólo en terminos de variables
no básicas. Como BxB+DxB=b premultiplicando por
B−1 tenemos una expresión para xB en función de xD
xB=B−1b−B−1DxB. Esta última puede
remplazarse en la función objetivo cBTxB+cDTxD
que da cBTB−1b+(cDT−cBTB−1D)xD.
Que puede reescribirse como
con zj=cB(B−1D)j.
Como cada xi es no negativa y buscamos una xj para que no sea 0,
la expresión anterior puede disminuir sólo si se hace básica una
xj (j∈ D) tal que (cj−zj)<0.
Por esto buscamos entre los coeficientes (cj−zj) el que sea más negativo,
buscando disminuir cTx al máximo. Si para todo j∈ D
resulta que cj−zj≥ 0 no hay forma de
disminuir la función objetivo cambiando las variables básicas, así que
tenemos un óptimo.
Note que en la tabla simplex los coeficientes (cj−zj) están justamente
en la última fila:
| I |
B−1D |
B−1b |
| 0 |
cDT−cBTB−1D |
−B−1b |
Para elegir la variable que deja de ser básica, una vez elejida xj
como la que ingresara, debemos asegurar que se logra una solución básica
factible.
Como B es base podemos expresar dj como combinación lineal de
las columnas de B: dj=Σi∈ Bbiyij
Como queremos que en los términos de la sumatoria ninguno de los
coeficientes xi−є yij se haga negativo
podemos escoger є que cumpla para todo i:
xi−є yij≥ 0 es decir є ≤ xi/yij.
Como además queremos que al menos uno de esos términos sea 0, escogemos:
y de la base de básicos sacamos la variable xp cuyo indice p logra
tal minimización. Si tal mínimo se alcanza para varias variables,
se trata de una solución degenerada y podemos escoger cualquier de
ellas. Si no hay yij positivos se trata de un óptimo no acotado.
Note que para expresar el vector dj como combinación lineal de la
base: dj=b1y1j+...bmymj i.e
By=dj o premultiplicando por B−1
y=B−1dj Así que los coeficientes se encuentran en
la j-esima columna de la matriz B−1D la cual aparece en la tabla
simplex:
| I |
B−1D |
B−1b |
| 0 |
cDT−cBTB−1D |
−B−1b |
y así hemos deducido las dos reglas del método simplex antes introducidas
para cambiar las varibles básicas.
1.3.2 Lecturas recomendadas
La interpretación geométrica es adaptada del Capítulo 2
de [4] y del capítulo 2 de [6].
El método de las dos fases y la deducción de las reglas del método
simplex son adaptados del capítulo 3 de
[6].
1.3.3 Ejercicios
-
(Adaptado de ejercicio 3.3.1 de [4])
Dado un problema de programación lineal de la forma:
| min |
cTx |
| sujeto a |
Ax≤ b |
| |
x≥ 0 |
-
(Adaptado de ejericio 2.3 de [6]) Una refinería de petróleo tiene
dos fuentes de petróleo bruto: crudo ligero, que cuesta 35
euros por barril, y crudo pesado, 30 euros por barril. A partir del crudo, la
refinería produce gasolina y combustibles para calefacción y
para turbinas en las catnidades por barril indicadas en la tabla
siguiente:
| |
Gasolina |
Combustible |
Combustible |
| |
|
para calefacción |
para turbinas |
| Crudo ligero |
0.3 |
0.2 |
0.3 |
| Crudo pesado |
0.3 |
0.4 |
0.2 |
La refinería ha contratado una provisión de 900000 barriles de gasolina,
800000 barriles de combustible para calefacción y 500000 barriles de
combustible para turbinas. La refinería desea calcular las cantidades
de crudo ligero y pesado que tiene que comprar para poder cubrir sus
necesidades al costo mínimo. Formúlese este problema como un problema
de programación lineal.
1.4 Ciclado y Dualidad
Indicadores de logro:
-
INDICADOR: Conoce un método para evitar ciclado con Simplex
- INDICADOR: Puede formular el dual de un problema de programación lineal
Prevención de ciclado
Dualidad
1.4.2 Lecturas recomendadas
El método de prvención de ciclado puede consultarse en
[4]
1.4.3 Ejercicios
-
(Ejercicio 1.1.7 de [4]) Un fabricante de acero produce 4 tamaños
de vigas en I: pequeño, mediano, grande y exra grande. Estas vigas se
pueden producir en cualquiera de tres tipos de máquinas: A, B y C.
A continuación se indican las longitudes (en pies) de las vigas I que
pueden producir las máquinas por hora.
| Viga |
A |
B |
C |
| Pequeña |
300 |
600 |
800 |
| Mediana |
250 |
400 |
700 |
| Larga |
200 |
350 |
600 |
| Extra larga |
100 |
200 |
300 |
Supóngase que cada máquina se puede usar hasta 50 horas por semana
y que los costos de operación por hora de estas máquinas son
$30, $50 y $80 respectivamente. Supóngase, además, que semanalmente
se requieren 10,000, 8,000, 6,000 y 6,000 pies de los distintos tamaños
de las vigas I. Formular el problema de programación de
máquinas como un programa lineal.
-
(Ejercicio 2.5 de [4]) Supongase que
a1,a2,...,an forman base En y
y=λ1a1+λ2a2+...+λnan
con λj=0. Demuestre que a1,...,aj−1,
y aj+1,...,an no forman una base de En.
-
(Ejercicio 2.7 de [4]) Sea
en donde B es una matriz m× m invertible, I es una matriz
identidad de k× k, 0 es
una matriz cero de m× k, y T es una matriz arbitraria
k× m. Demostrar que A es invertible y que
-
(Ejercicio 2.11 de [4]) Demostrar que si A y B son
matrices n× n invertibles, entonces (AB)−1=B−1A−1.
-
(Ejercicio 2.15 de [4]) Sea B una matriz invertible con elementos
no negativos, demostrar que cada renglón de B−1 tienen al menos un
elemento positivo.
-
(Ejercicio 2.46 de [4]) Sea X={x : Ax=b,
x≥ 0} en donde A es una matriz m× n con
rango m, demostrar que d es una dirección extrema de X si
y sólo si, d es un múltiplo positivo del vector
(−yjT,0,0,...,1,0,...,0)T en donde el 1 aparece en
la posición j y
| yj |
= |
B−1aj≥ 0 |
| A |
= |
[B, N] |
| aj |
= |
columna de N |
| −x1+x2+x3 |
= |
2 |
| −x1+2x2+x4 |
= |
6 |
| x1,x2,x3,x4≥ 0 |
-
(Ejercicio 2.51 de [4]) Determinar todos los puntos extremos
y las direcciones extremas del siguiente conjunto poliédrico:
X={(x1,x2,x3,x4):x1,x2,x3,x4≥ 0, −x1+x2+x3=1, x2+x4=2}
Representar x=(1,3/2,1/2,1/2) como una combinación
convexa de los puntos extremos de X más una combinación lineal no negativa de
las direcciones extremas de X.
-
(Ejercicio 3.21 de [4])
Una empresa hace tres productos 1, 2 y 3. Cada producto requiere
de un tiempo de producción en tres departamentos, como se muestra
en la siguiente tabla:
| Producto |
Departamento 1 |
Departamento 2 |
Departamento 3 |
| 1 |
3 hr/unidad |
2 hr/unidad |
1 hr/unidad |
| 2 |
4 hr/unidad |
1 hr/unidad |
3 hr/unidad |
| 3 |
2 hr/unidad |
2 hr/unidad |
3 hr/unidad |
En cada uno de los tres departamentos se dispone de 600, 400 y 300 horas de
producción, respectivamente. Si cada uno de los productos 1, 2 y 3 contribuye
con una ganancia de $2, $4 y $2.5 respectivamente, determinar la
combinación óptima de productos.
1.5 Condiciones de Kuhn Tucker
Indicadores de logro:
-
INDICADOR: Aplica condiciones de Kuhn Tucker en problemas de programación lineal
Multiplicadores de Lagrange
Si x* es punto regular de h(x*) y
x* es solución extrema de
f(x) sujeto a h(x)=0,
entonces:
∃λ ∈ Rn
∇ f(x*)=λ∇ h(x*)
Ejemplo: Encuentre los valores extremos de la función
f(x,y)=x2+2y2 en el circulo x2+y2=1
Solución: Nos piden los valores extremos de f sujetos a la
restricción h(x,y)=x2+y2−1=0.
Usando multiplicadores de Lagrange, resolvemos las ecuaciones
| ∇ f(x,y)=λ∇ h(x,y) |
| h(x,y)=0 |
o bien como:
-
2x=2xλ
- 4y=2yλ
- x2+y2=1
De 2x=2xλ tenemos x=0 o λ=0, entonces
x2+y2=1 da y=± 1.
Si λ=1, entonces y=0 de 4y=2yλ, de modo que
x2+y2=1 da x=±1.
Por tanto, f tiene posibles valores extremos en los
puntos (0,1), (0,-1), (1,0) y (-1,0).
Al evaluar f en estos cuatro puntos, encontramos que:
f (0,1) =2, f (0,−1)=2, f (1,0) =1,
f (−1,0)=1
Por tanto, los valores máximo y mínimo respectivamente de f en el
círculo x2+y2=1 son f (0,±1)=2 y f (±1,0)=1.
Condiciones de Kuhn Tucker
Si x* es solución de
| min |
f(x) |
| s.a. |
h(x)=0 |
| |
g(x)≤0 |
| ∇f(x*)+λT∇g(x)
+μT∇h(x*)=0 |
| μTg(x*)=0 |
Condiciones de Kuhn Tucker para problemas de programación lineal
equivale a
Las funciones y gradientes involucrados son:
| f(x)=cTx |
, |
∇ f=cT |
| h(x)=Ax−b |
, |
∇ h=A |
| g(x)=−x |
, |
∇ g=−I |
Buscamos λ∈Rm,
μ∈Rn, x*∈Rp que satisfagan
| cT+λTA −μT(−I)=0 |
| μT(−x)=0 |
equivale a
| cT+λTA −μT=0 |
| μT(x*)=0 |
| Ax*=b |
| x*≥0 |
Con
λ∈Rn,μ∈Rn,
μ≥0
1.5.2 Lecturas recomendadas
Las condiciones de Kuhn Tucker para problemas no lineales pueden
ser consultadas en [6].
Su uso en el caso de problemas de programación lineal puede
consultarse en [4].
1.5.3 Ejercicios
-
(Ejercicio adaptado de [3]) Calcule la distancia máxima y mínima del
origen a la curva 5x2+6xy+5y2=8. Muestre que los puntos donde se alcanzan
máximo y mínimo son regulares.
-
A partir de la formulación general del teorema de Kuhn Tucker, deducir
las condiciones para un problema de programación lineal del estilo:
| max |
cTx |
| sujeto a |
Ax ≥ b |
| |
x≥ 0 |
-
(Ejercicio 5.42 de [4]) Considerese el siguiente problema:
| max |
x1−2x2+x3 |
| sujeto a |
x1+x2+x3≤ 6 |
| |
2x1+x2≤ 4 |
| |
−x1+2x2−x3≤ 4 |
| |
x1, x2, x3≥ 0 |
-
(Ejercicio 5.41 de [4]) Considérese el problema: Minimizar
cTx sujeta a Ax=b, x≥ 0.
Ignorando la cuestión de la factibilidad, demostrar que empezando en
cualquier punto x, la dirección con norma 1, que es aquella que
mejora más la función objetivo, es −c /|c|.
-
(Ejercicio 5.39 de [4]) un fabricante produce dos artículos con
ganancias por unidad de $10 y $15. Cada unidad del artículo 1 usa 4
horas-hombre y 3 horas-máquina. Cada unidad del artículo 2 usa 7 horas-hombre
y 6 horas-máquina. Si el total disponible de horas-hombre y de
horas-máquina es de 300 y 500 respectivamente, encontrar la solución óptima
y verificarla usando las condiciones de Kuhn-Tucker. Dar una interpretación
económica de las condiciones de Kuhn-Tucker en el punto óptimo.
-
(Adaptado del ejercicio 1.5 de [4]) Una compañia desea
planificar la producción de dos de sus artículos que tienen demanda de
temporada en un período de 12 meses. La demanda mensual conocida del
artículo 1 es de 100,000 unidades durante los meses de octubre, noviembre
y diciembre y de 10,0000 unidades el resto del año. El artículo 2
tiene una demana de 50,0000 durante los meses de febrero a octubre y
de 15,000 durante los meses restantes. Suponga que el costo por unidad
para producir los artículos 1 y 2 es de $5 y $8 respectivamente, siempre y
cuando se fabriquen antes de junio. Después de junio, los costos por unidad
se reducen a $4.50 y $7 debido a la instalación de un mejor sistema de
fabricación. El número total de unidades de los artículos 1 y 2 que pueden
fabricarse durante cualquier mes particular no puede ser mayor de
120,000. Además, cada unidad del artículo 1 ocupa 2 pies cúbicos de
almacén y cada unidad del artículo 2 ocupa 4 pies cúbicos. Supóngase
que el espacio máximo de almacén asignado a estos artículos es de 150,000
pies cúbicos y que el costo de arrendamiento por pie cúbico calculado al
final de cada mes es de $0.10. Formule el problema de planeación de
producción de tal manera que la producción total y los costos de inventario
sean mínimos.
- 1
- La
convención que empleamos para este vector r
es la introducida en [6]. En [4] y
[9] en problemas de minimización se usa el inverso
multiplicativo de cada coeficiente
de la función objetivo, el valor z da el valor de la función
objetivo y la regla para elegir próxima variable (columna) que
será básica es la que tenga el coeficiente en r con el máximo
valor positivo.
- 2
- Deben introducirse tantas variables artificiales
como columnas falten para completar una submatriz identidad en la tabla
simplex. En el caso extremo (que es el supuesto en esta guía) se requieren
m variables artificiales.







