Capítulo 5 Grafos y redes

LOGRO: Emplea grafos para plantear problemas y algoritmos sobre grafos para resolverlos
LOGRO: Emplea redes para plantear problemas y algoritmos sobre estas para resolverlos

5.1 Ruta más corta y Flujo en redes

Indicadores de logro:

INDICADOR: Maneja definiciones de grafos
INDICADOR: Plantea y resuleve problemas en los que se requiera hallar la ruta más corta entre nodos de un grafo
INDICADOR: Plantea y resuleve problemas que puedan modelarse como minimizar costo de flujo en una red

5.1.1 Teoría

Definiciones de grafos

Definición 1 Un grafo es una pareja de vértices y arcos (V,A). Usualmente V={1,2,3,...,n} y cada arco es un conjunto con dos vertices, A={{i₁,i₂},{i₃,i₄},...,{i_n−1,i_n}} (Tengase en cuenta {a,b}={b,a}).

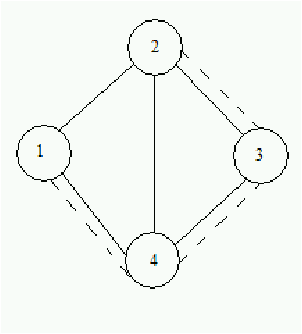
Figure 5.1: Ejemplo de grafo V={1,2,3,4}, A={{1,4}, {1,2}, {2,4}, {3,4}}

Definición 2 Una cadena es una sucesión de arcos de la forma {e₁,e₂},{e₂,e₃},{e₃,e₄},...,{e_p−1,e_p}

En la figura 5.1 {{1,4},{4,3},{3,2}} (Línea punteada).

Definición 3 Un ciclo es una cadena que inicia y termina en el mismo nodo.

Definición 4 Un grafo G es conexo si hay una cadena entre cualquier par de vértices.

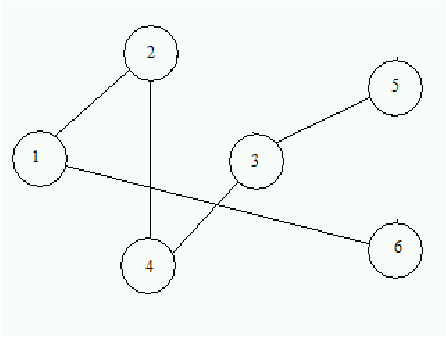
Figure 5.2: Ejemplo de grafo conexo

Definición 5 Un grafo G'=(V',A') es subgrafo de G=(V,A), (denotado G'⊂ G) cuando V'⊂ V y A'⊂ A

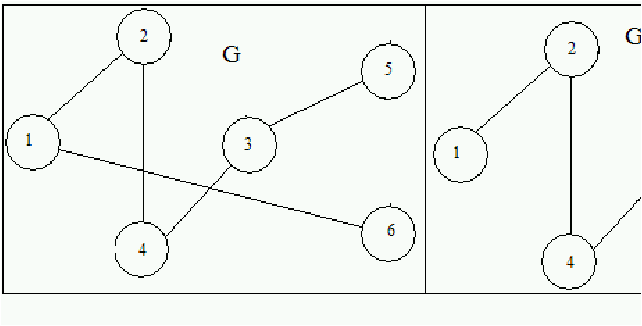
Figure 5.3: Ejemplo de subgrafo

Definición 6 Un subgrafo G' de un grafo G es árbol si G' es conexo y no tiene ciclos.

Ver figura 5.2.

Definición 7 Un árbol G' de un grafo G es árbol de expansión si llega a todos los vértices de G.

Ver figura 5.2.

Definición 8 El orden del grafo G=(V,A) es |V|

Teorema 1 Un grafo G es conexo si y solo si contiene un árbol de expansión.

Si G es conexo ⇒ contiene un árbol de expansión
Si G contiene un árbol de expansión ⇒ G es conexo.

Definición 9 En un grafo dirigido G =(V,A) el conjunto de arcos cumple A⊂ V× V. Si (i,j)∈ A decimos que el arco comienzo en i termina en j.

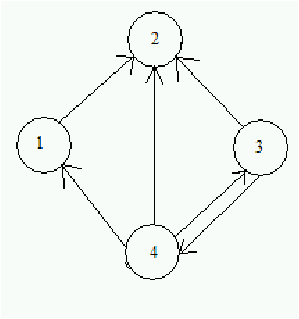
Figure 5.4: Ejemplo de grafo dirigido

Definición 10 Para definir grafo decorado requerimos un conjunto de etiquetas E. Se trata de una tripla G=(V,A,f) donde V y A tienen el significado usual (ya sea no dirigido o dirigido) y f es función f:A—→ E

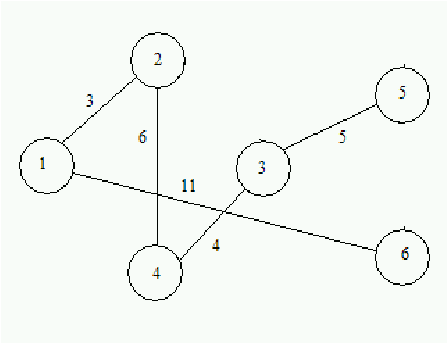
Figure 5.5: Ejemplo de grafo no dirigido decorado

Las definiciones de cadena, ciclo, conexidad y árbol se extiende a grafos dirigidos, pero sin tener en cuenta la dirección de cada arco (i.e mirando el grafo como si fuera no dirigido).

Definición 11 En un grafo dirigido una trayectoria es una sucesión de arcos de la forma: {(i₁,i₂),(i₂,i₃),(i₃,i₄)...(i_n−1,i_n)}

Definición 12 En un grafo dirigido un circuito es una trayectoria que comienza y termina en el mismo nodo.

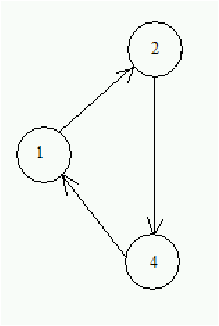
Figure 5.6: Ejemplo de un circuito

Árbol de expansión

Es posible econtrar un árbol de expansión en un grafo conexo con un algoritmo en el cual empleamos:

C_k es conjunto de nodos que lleva incluidos en el árbol en la iteración k.
C_k' es conjunto de nodos que aún hacen falta en la iteración k.

Paso 0: C₀= C₀'=V
Paso 1: Comenzar con cualquier nodo i en C₀' C₁={i} C₁'=V−{i}. Sea k=2.
Paso k: Seleccionar j^*∈ C_k−1' que produzca el arco más corto de un nodo en C_k−1 a un nodo en C_k−1'.
C_k=C_k−1 U {j^*}
C_k'=C_k−1'−{j^*}

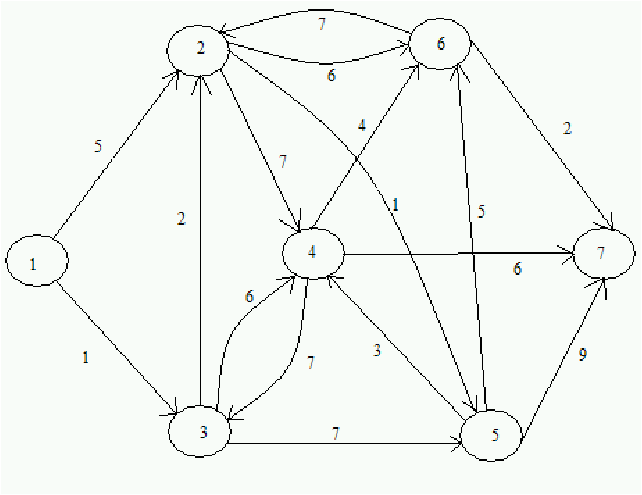
Figure 5.7: Ejemplo de grafo conexo en el que se puede hallar un árbol de expansión

Ruta más corta: Algoritmo de Dijkstra

Permite encontrar la distancia más corta entre un nodo y los demás nodos del arco. Por ejemplo para encontrar distancia más corta del nodo 1 a los demás nodos de

Paso 0. Escogemos el nodo 1 para comenzar
Paso 1.

1 2 3 4 5 6 7

Distancia - 5 1 - - - -

Nodo - 1 1 - - - -
Paso 2

1 2 3 4 5 6 7

Distancia - 3 1 7 8 - -

Nodo - 3 1 3 3 - -
Paso 3

1 2 3 4 5 6 7

Distancia - 3 1 7 4 9 -

Nodo - 3 1 3 2 2 -
Paso 4

1 2 3 4 5 6 7

Distancia - 3 1 7 4 9 11

Nodo - 3 1 3 2 2 6

Por ejemplo la distancia mas corta al nodo 7 es 11 y su trayectoria es 1-3-2-6-7.

Ruta más corta: Algoritmo de Floyd

El algoritmo de Floyd permite determinar las distnacias mínimas entre cualquier par de nodos de un grafo. La ídea central es que para ir de i a k resulta mejor pasar primero por j si d_ij+d_jk≥ d_ik, y en ese caso se remplaza la trayectoria i—→ k por i—→ j—→ k.

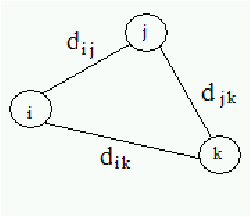
Figure 5.8: Posibilidades para ir de i a k

Paso 0

D₀=

⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣

	1	2	3	⋯	j	⋯	n
1	−	d₁₂	d₁₃	⋯	d_1j	⋯	d_1n
2	d₂₁	−	d₂₃	⋯	d_2j	⋯	d_2n
3	d₃₁	d₃₂	−	⋯	d_3j	⋯	d_3n
⋮
i	d_i1	d_i2	d_i3	⋯	d_ij	⋯	d_in
⋮
n	d_n1	d_n2	d_n3	⋯	d_nj	⋯	d_nn

⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦

S₀=

⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣

	1	2	3	⋯	j	⋯	n
1	−	2	3	⋯	j	⋯	n
2	1	−	3	⋯	j	⋯	n
3	1	2	−	⋯	j	⋯	n
⋮
i	1	2	3	⋯	j	⋯	n
⋮
n	1	2	3	⋯	j	⋯	n

⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦

Paso k (k≤ n) defina D_k y S_k usando D_k−1 y S_k−1 hacer “pivote” en elemento (k,k).

Para todo i,j ,i≠ k ,j≠ k, i≠ j si en D_k−1 d_ik+d_kj<d_ij poner d_ik+d_kj en pocisión (i,j) de D_k y poner k en posición (i,j) de S_k. En otro caso [D_k]_ij=[D_k−1]_ij y [S_k]_ij=[S_k−1]_ij.

Flujo en redes

Definición 13 Una red es un grafo con etiquetas en los arcos que representan costos y con flujos x_ij asociadas a cada arco (i,j).

El problema de la ruta más corta entre un nodo fuente s y uno destino t en un grafo dirigido con costos G=(V,A,C) con V = {1,2,3,......n} y A = {(i₁,i₂),(i₂,i₃),(i₃,i₄)⋯ (i_k,i_k+1)} y C_ij∈ C costo del arco (i,j), puede plantearse como red con flujos x_ij (del nodo i al j) en los que cada x_ij≥0 puede ser 0 o 1. En la red se buscaría minimizar el costo total de los flujos por cada arco, añadiendo sólo un flujo de entrada unitario en el nodo s y un flujo unitario de salida en el nodo t.

Al plantearlo como problema de programación lineal, tenemos como función objetivo: min Σ₍i,j)∈ A x_ij*C_ij con restricciones de la forma:

Flujo que sale del nodo i = flujo que entra al nodo i

x₁2+x₁4=1

x₁2−x₂3=0

−x₂3−x₄3−x₅3=−1

x₄3+x₄5−x₁4=0

x₅3−x₄5=0

Flujo de costo mínimo

El problema presentado en la sección anterior es un caso particular del problema general de minimizar flujo en una red.

Para plantearlo, cada nodo tiene un b_i que es 0, excepto para nodos fuentes (b_i>0) y para nodos sumidero (b_i<0). Debe cumplirse una condición de equilibrio: Σ_i=1ⁿbi=0.

De forma que el problema de flujo de costo mínimo es:

min

(

i,j)∈ A x_ij*C_ij

s.a

j=1

x_ij

−

k=1

x_ki = b_i

i=1,2,...n

La matriz A asociada tiene varias propiedades:

Una base para el problema de flujo con costo minimo en un red esta caracterizado por un árbol de expansion enraizado.
Si los b_i son enteros, entonces los flujos de la solución óptima son enteros.
Es totalmente unimodular (i.e el determinante de cualquier submatriz es 1 o 0 o -1).
Toda base es triangular.

5.1.2 Lecturas recomendadas

La presentación de grafos se basa especialmente en la guía 1 de [10] y en [9]. La presentación de de flujo en redes se basa especialmente en [4].

5.1.3 Ejercicios

En el capítulo 1 de [10], además de definiciones de grafos se presenta el “Lema de los apretones de manos”. Demuestrelo.
(Adaptado de ejercicio 6.2A.4 de [9]) En la figura 5.9 se ven las distancias, en millas, de las conexiones factibles que unen nueve pozos subterraneos de agua con un punto de entrega. Como la ubicación del pozo 1 es la más cercana al punto de entrega, tiene capacidad de bombeo y de almacenamiento suficiente para bombear la producción de los ocho pozos restantes hasta el punto de entrega. Determine la red mínima de tubería que una las bocas de los pozos con el punto de entrega.

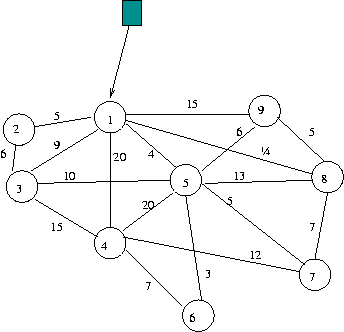
Figure 5.9: Distancias entre pozos de agua
(Adaptado de ejercicio 6.3A.2 de [9]) La figura 5.10 muestra la red de comunicaciones entre dos estaciones 1 y 7.

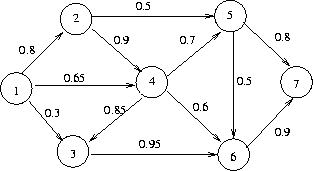
Figure 5.10: Grafo con probabilidad de funcionamiento de enlaces en una red eléctrica

La probabiliad de que un enlace de la red funcione sin fallar se ve en cada arco. Los mensajes se mandan de la estación 1 a la estación 7, y el objetivo es determinar la ruta que maximice la probabilidad de una buena transmisión. Formule el caso como modelo de ruta más corta y resulevalo.
(Ejemplo 6.3.3 de [9]) Un garrafón de 8 galones se llena con un líquido. Se cuenta con un botellón de 5 y uno de 3 galones, y se quiere dividir los 8 galones de líquido en dos partes iguales, usando los tres garrafones. No se permite usar algún otro medidor. ?'Cuál es la cantidad mínima de vertidos necesarios para lograr este resultado?
(Adaptado de ejercicio 5.5A.5 de [9]) Acerca de la red presentada en la figura 5.11, los distintos nodos representan estaciones de bombeo y recepeción. En la red se ven las distancias entre las estaciones. El costo de transporte por galón, entre dos nodos, es directamente proporcional a la longitud del ducto. Formule el modelo de flujo de costo mínimo correspondiente y determine la solución óptima.

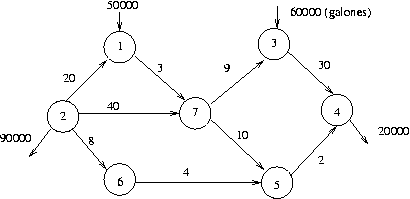
Figure 5.11: Grafo con distancias entre estaciones de una red

5.2 Flujo maximal en una red

Indicadores de logro:

INDICADOR: Plantea y resuleve problemas en los que se requiera maximizar el flujo en una red

5.2.1 Teoría

Planteamineto del problema de flujo maximal en una red

Algoritmo de solución

Cortes y teorema de flujo maximal corte mínimo

5.2.2 Lecturas recomendadas

La presentación se basa especialmente en [9] y en [6].

5.2.3 Ejercicios

(Ejercicio 6.4B.5 de [9]) De tres silos se transporta alimento para pollos a cuatro granjas. Algunos de los silos no pueden mandar en forma directa a algunas de las granjas. Las capacidades de las demás rutas se limitan por la cantidad de camiones disponibles y la cantidad de viajes que se hacen diario. La tabla siguiente muestra las cantidades diarias de oferta en los silos, y la demanda en las granjas (en miles de libras). Los elementos de las celdas de la tabla especifican las capacidades diarias de las rutas correspondientes.

Granja

1 2 3 4

1 30 5 0 40 20

Silo 2 0 0 5 90 20

3 100 40 30 40 200

200 10 60 20 200
1. Determine la solución que satisfaga la máxima parte de la demanda.
2. La solución propuesta ¿satisfacerá toda la demanda en las granjas?
(Adaptado de ejercicio 6.4B.6 de [9]) En el problema anterior suponga que se permite transbordo entre los silos 1 y 2 y los silos 2 y 3. También suponga que se permite transborod entre las granjas 1 y 2, 2 y 3, 3 y 4. La capacidad diaria en las dos direcciones, de las rutas propuestas de transporte es 50 (mil) lb. ¿Qué efecto tiene el trasbordo sobre las demandas no satisfechas en las granjas?

			Granja
		1	2	3	4
	1	30	5	0	40	20
Silo	2	0	0	5	90	20
	3	100	40	30	40	200
		200	10	60	20	200

	1	2	3	4	5	6	7
Distancia	-	5	1	-	-	-	-
Nodo	-	1	1	-	-	-	-

	1	2	3	4	5	6	7
Distancia	-	3	1	7	8	-	-
Nodo	-	3	1	3	3	-	-

	1	2	3	4	5	6	7
Distancia	-	3	1	7	4	9	-
Nodo	-	3	1	3	2	2	-

	1	2	3	4	5	6	7
Distancia	-	3	1	7	4	9	11
Nodo	-	3	1	3	2	2	6